
【题目】已知二次函数y=x2﹣2mx+4m﹣8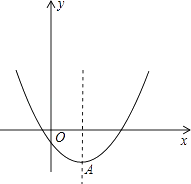
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
【答案】
(1)解:二次函数y=x2﹣2mx+4m﹣8的对称轴是:x=m.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)解:如图:
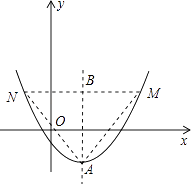
顶点A的坐标为(m,﹣m2+4m﹣8)
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°= ![]() =
= ![]() ,
,
则AB= ![]() BM=
BM= ![]() BN,
BN,
设BM=BN=a,则AB= ![]() a,
a,
∴点M的坐标为(m+a, ![]() a﹣m2+4m﹣8),
a﹣m2+4m﹣8),
∵点M在抛物线上,
∴ ![]() a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
整理得:a2﹣ ![]() a=0
a=0
得:a= ![]() (a=0舍去)
(a=0舍去)
所以△AMN是边长为2 ![]() 的正三角形,
的正三角形,
S△AMN= ![]() ×2
×2 ![]() ×3=3
×3=3 ![]() ,与m无关;
,与m无关;
(3)解:当y=0时,x2﹣2mx+4m﹣8=0,
解得:x=m± ![]() =m±
=m± ![]() ,
,
∵抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,
∴(m﹣2)2+4应是完全平方数,
∴m的最小值为:m=2.
【解析】(1)首先依据二次函数的对称轴公式求得抛物线的对称轴为x=m,由于a>0可得到抛物线的开口向上,故此在对称轴的左边y随x的增大而减小,从而可得到关于m的不等式;
(2)在抛物线内作出正三角形,顶点A的坐标为(m,﹣m2+4m﹣8),设BM=BN=a,则AB= ![]() a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
(3)首先令y=0,从而可求出抛物线与x轴的两个交点的坐标,然后确定整数m的值即可.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A的坐标为(-4,4),点B的坐标为(0,2).

(1)求直线AB的解析式;
(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC-OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M(-4,0)和N(2,0)是x轴上的两个点,点P是直线AB上一点.当△PMN是直角三角形时,请求出满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
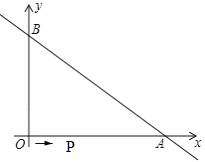
【题目】如图,直线![]() 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)则A点的坐标为_____,B两点的坐标为______;
(2)当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为______;
(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们把对非负实数![]() “四舍五入”到个位的值记为
“四舍五入”到个位的值记为![]() ,
,
即当![]() 为非负整数时,若
为非负整数时,若![]() ,则
,则![]() .
.
例如:![]() ,
,![]() ,….
,….
请解决下列问题:
(1)![]() ______;
______;
(2)若![]() ,则实数
,则实数![]() 的取值范围是_________;
的取值范围是_________;
(3)①![]() ;
;
②当![]() 为非负整数时,
为非负整数时,![]() ;
;
③满足![]() 的非负实数
的非负实数![]() 只有两个.其中结论正确的是_____(填序号)
只有两个.其中结论正确的是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.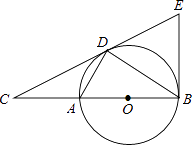
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校七年级4个班共180人的体质健康情况,从各班分别抽取同样数量的男生和女生组成一个样本,如图是根据样本绘制的条形图和扇形图.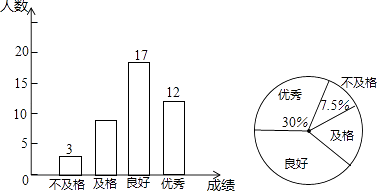
(1)本次抽查的样本容量是 .
(2)请补全条形图和扇形图中的百分数;
(3)请你估计全校七年级共有多少人优秀.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com