
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A������Ϊ��-4��4������B������Ϊ��0��2����

��1����ֱ��AB�Ľ���ʽ��
��2���Ե�AΪֱ�Ƕ�������CAD=90��������AC��x��ĸ������ڵ�C������AD��y��ĸ������ڵ�D������CAD���ŵ�A��תʱ��OC-OD��ֵ�Ƿ����仯�������䣬�������ֵ�����仯��������ı仯��Χ��
��3����ͼ2����M��-4��0����N��2��0����x���ϵ������㣬��P��ֱ��AB��һ�㣮����PMN��ֱ��������ʱ��������������������е�P�����꣮
���𰸡���1��ֱ��AB�Ľ���ʽΪ��y=-![]() x+2����2����2�����䣮���ɼ���������3����P������Ϊ��-4��4����2��1����-
x+2����2����2�����䣮���ɼ���������3����P������Ϊ��-4��4����2��1����-![]() ��
��![]() +2����
+2����![]() ��-
��-![]() +2����
+2����
��������
��1����ֱ��AB����ʽΪy=kx+b����A��B��������г������飬���������Ľ�õ�k��b��ֵ������ȷ����ֱ��AB����ʽ��
��2������CAD���ŵ�A��תʱ��OC-OD��ֵ���䣬����Ϊ����A��AE��ֱ��x�ᣬAF��ֱ��y�ᣬ����ͬ�ǵ������ȵõ�һ�Խ���ȣ����A������õ�AE=AF��������ֱ֪����ȣ�����ASA�õ�������AEC��������AFDȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�EC=FD���������OC-OD��ֵ���ɣ�
��3��������������ǣ��ٵ�MΪֱ�Ƕ���ʱ����NΪֱ�Ƕ���ʱ����PΪֱ�Ƕ���ʱ���ֱ����P���꼴�ɣ�
��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�ߵ�A��-4��4������B��0��2����ֱ��AB�ϣ�
��![]() ��
��
��ã� ��
��
��ֱ��AB�Ľ���ʽΪ��y=-![]() x+2��
x+2��
��2�����䣮�������£�
����A�ֱ���x�ᣬy��Ĵ��ߣ�����ֱ�ΪE��F�����ͼ1�����ɵá�AEC=��AFD=90����

�֡ߡ�BOC=90����
���EAF=90��������DAE+��DAF=90����
�ߡ�CAD=90��������DAE+��CAE=90����
���CAE=��DAF��
��A��-4��4����
��OE=AF=AE=OF=4��
����AEC����AFD��
 ��
��
���AEC�ա�AFD��ASA����
��EC=FD��
��OC-OD=��OE+EC��-��FD-OF��=OE+OF=8��
��OC-OD��ֵ�������仯��ֵΪ8��
��3���ٵ�MΪֱ�Ƕ���ʱ����P�ĺ�����Ϊ-4��
�ߵ�P��ֱ��AB�ϣ�
��x=-4����y=-![]() x+2�ã�y=4��
x+2�ã�y=4��
���P������ΪP��-4��4����
�ڵ�NΪֱ�Ƕ���ʱ����P�ĺ�����Ϊ2��
�ߵ�P��ֱ��AB�ϣ�
��x=2����y=-![]() x+2�ã�y=1��
x+2�ã�y=1��
���P������ΪP��2��1����
�۵�PΪֱ�Ƕ���ʱ��
�ߵ�P��ֱ��AB�ϣ������P������Ϊ��x��-![]() x+2����
x+2����
��MP2=��x+4��2+��-![]() x+2��2��NP2=��x-2��2+��-
x+2��2��NP2=��x-2��2+��-![]() x+2��2��
x+2��2��
��Rt��PMN��MP2+NP2=MN2��MN=6��
�ࣨx+4��2+��-![]() x+2��2+��x-2��2+��-
x+2��2+��x-2��2+��-![]() x+2��2=62��
x+2��2=62��
��ã�x1=-![]() ��x2=
��x2=![]() ��
��
��P��-![]() ��
��![]() +2����
+2����![]() ��-
��-![]() +2����
+2����
�����������������������е�P������Ϊ��-4��4����2��1����-![]() ��
��![]() +2����
+2����![]() ��-
��-![]() +2����
+2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=40�㣬��ABC����ǡ�CBD��ƽ����BE��AC���ӳ����ڵ�E��
��1�����CBE�Ķ�����
��2������D��DF��BE����AC���ӳ����ڵ�F�����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() ����������ֱ���
����������ֱ���![]() ��
��![]() ��
��![]()
��1��������������ͼ�У��������ƽ��ֱ������ϵ��
��2����![]() ����ƽ�ƺ��Ӧ��Ϊ
����ƽ�ƺ��Ӧ��Ϊ![]() ����������
����������![]() ��ͬ����ƽ�Ƶõ�������
��ͬ����ƽ�Ƶõ�������![]() .
.
�ٻ���ƽ�ƺ��������![]() ��
��
����![]() ����һ��
����һ��![]() ��������ƽ�ƺ�Ķ�Ӧ��Ϊ
��������ƽ�ƺ�Ķ�Ӧ��Ϊ![]() ���ú�
���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��![]() �����ꣻ(ֱ��д���������)
�����ꣻ(ֱ��д���������)
����������![]() �����.
�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����������������˾ӳɶ�����������һ���㳡����ֲ�ס������ֻ��ܣ����г����飬���ֻ��ܵ���ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ��
��1��ֱ��д����0��x��300��x��300ʱ��y��x�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����1200m2�������ֻ��ܵ���ֲ���������200m2���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����뾶Ϊ6��ԲO��һ��A��ԲO������l��PΪԲO��һ�����㣬��PH��l�ڵ�H������PA�����PA=x��AH=y����ô����ͼ���У��ܴ��±�ʾy��x�ĺ�����ϵ���ǣ� ��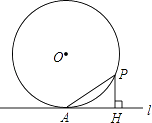
A.
B.
C.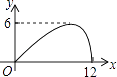
D.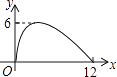
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ӳ��У�![]() �㣩����������
�㣩����������![]() ����С��ң�
����С��ң�![]() �㣩����������
�㣩����������![]() ����С�żң�
����С�żң�![]() �㣩��Ȼ���ֻ�ͷ������
�㣩��Ȼ���ֻ�ͷ������![]() ����С�¼ң�
����С�¼ң�![]() �㣩�����ص����У�
�㣩�����ص����У�
��1���Գ���Ϊԭ�㣬����Ϊ��������![]() ��ʾ
��ʾ![]() ���������ᣬ���ڸ������ϱ�ʾ
���������ᣬ���ڸ������ϱ�ʾ![]() ��
��![]() ��
��![]() ��
��![]() ��λ�ã�
��λ�ã�
��2��С�¼ң�![]() �㣩��С��ң�
�㣩��С��ң�![]() �㣩�ж�Զ��
�㣩�ж�Զ��
��3��������շѱ����£�![]() ���ڰ���
���ڰ���![]() �շ�
�շ�![]() Ԫ������
Ԫ������![]() ���ְ�ÿǧ��
���ְ�ÿǧ��![]() Ԫ�շѣ���ӳ��г������ص�����һ�����Ѷ���Ԫ��
Ԫ�շѣ���ӳ��г������ص�����һ�����Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������ס������ֻ��ܣ����������ֻ���20�裬���ֻ���50�裬��Ҫ900Ԫ�����������ֻ���40�裬���ֻ���30�裬��Ҫ960Ԫ��
��1�����ס������ֻ���ÿ��������Ԫ��
��2���û��깺���ף������ֻ��ܹ�100�裬���ֻ���ÿ���ۼ�20Ԫ�����ֻ���ÿ���ۼ�16Ԫ���ָû����100�軨��ȫ���۳�������������480Ԫ�������ٹ������ֻ��ܶ����裿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��2mx+4m��8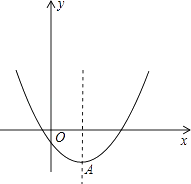
��1����x��2ʱ������ֵy��x���������С����m��ȡֵ��Χ��
��2����������y=x2��2mx+4m��8�Ķ���AΪһ���������������ߵ��ڽ���������AMN��M��N�����ڒ������ϣ������ʣ���AMN���������m�صĶ�ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
��3����������y=x2��2mx+4m��8��x�ύ��ĺ������Ϊ������������m����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com