
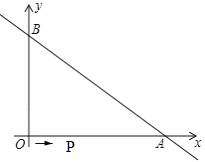
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гызјБъжсЗжБ№НЛгкAЁЂBСНЕуЃЌOA=8ЃЌOB=6ЃЎЖЏЕуPДгOЕуГіЗЂЃЌбиТЗЯпOЁњAЁњBвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕНДяBЕуЪБдЫЖЏЭЃжЙЃЎ
гызјБъжсЗжБ№НЛгкAЁЂBСНЕуЃЌOA=8ЃЌOB=6ЃЎЖЏЕуPДгOЕуГіЗЂЃЌбиТЗЯпOЁњAЁњBвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕНДяBЕуЪБдЫЖЏЭЃжЙЃЎ
(1)дђAЕуЕФзјБъЮЊ_____ЃЌBСНЕуЕФзјБъЮЊ______ЃЛ
(2)ЕБЕуPдкOAЩЯЃЌЧвBPЦНЗжЁЯOBAЪБЃЌдђДЫЪБЕуPЕФзјБъЮЊ______ЃЛ
(3)ЩшЕуPЕФдЫЖЏЪБМфЮЊtУы(0ЁмtЁм4)ЃЌЁїBPAЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃКВЂжБНгаДГіЕБS=8ЪБЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ8ЃЌ0ЃЉЃЛЃЈ0ЃЌ6ЃЉЃЛЃЈ2ЃЉЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉS=24-6tЃЈ0ЁмtЁм4ЃЉЃЌPЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнOAКЭOBЕФГЄЖШПЩЧѓГіAЁЂBСНЕуЕФзјБъЃЛ
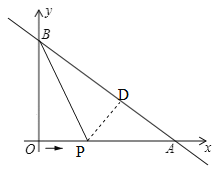
ЃЈ2ЃЉЙ§PзїPDЁЭBAгкDЃЎгЩНЧЦНЗжЯпЕФаджЪЕУЕНPD=OPЃЌЭЈЙ§жЄУїRtЁїBDPЁеRtЁїBOPЃЌЕУЕНBD=OB=6ЃЌDA= 4ЃЎдкRtЁїPDAжаЃЌгЩЙДЙЩЖЈРэМДПЩЧѓЕУНсТлЃЛ
ЃЈ3ЃЉЕБ0ЁмtЁм4ЪБЃЌPдкЯпЖЮOAЩЯдЫЖЏЃЌгЩOP=2tЃЌPA=8Ѓ2tЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЌЕБS=8ЪБЃЌДњШыНтЮіЪНМДПЩЧѓЕУtЕФжЕЃЌНјЖјЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпOA=8ЃЌOB=6ЃЌЁрAЃЈ8ЃЌ0ЃЉЃЌBЃЈ0ЃЌ6ЃЉЃЎ
ЃЈ2ЃЉЙ§PзїPDЁЭBAгкDЃЎ
ЁпBPЦНЗжЁЯOBAЃЌЁрPD=OPЃЎ
ЁпBP=BPЃЌЁрRtЁїBDPЁеRtЁїBOPЃЌЁрBD=OB=6ЃЎ
ЁпOA=8ЃЌOB=6ЃЌЁрBA=10ЃЌЁрDA=ABЃBD=10Ѓ6=4ЃЎ
дкRtЁїPDAжаЃЌЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃКOP=3ЃЌЁрPЃЈ3ЃЌ0ЃЉЃЎ
ЃЌНтЕУЃКOP=3ЃЌЁрPЃЈ3ЃЌ0ЃЉЃЎ
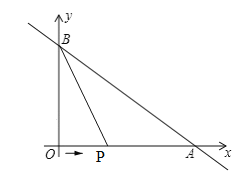
ЃЈ3ЃЉЁпOA=8ЃЌv=2ЃЌЁрt=8ЁТ2=4ЃЌЁрPДгOдЫЖЏЕНAЕФЪБМфЮЊ4УыЃЌЁрЕБ0ЁмtЁм4ЪБЃЌPдкЯпЖЮOAЩЯдЫЖЏЃЎ
OP=2tЃЌPA=8ЃOP=8Ѓ2tЃЌS=SЁїBAP=![]() PAOB=
PAOB=![]() ЃЈ8-2tЃЉ6=24Ѓ6tЃЎ
ЃЈ8-2tЃЉ6=24Ѓ6tЃЎ
ЕБS=8ЪБЃЌ8=24Ѓ6tЃЌНтЕУЃКt=![]() ЃЌЁрOP=2t =2ЁС
ЃЌЁрOP=2t =2ЁС![]() =
=![]() ЃЌЁрPЃЈ
ЃЌЁрPЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
Д№ЃКS= 24Ѓ6tЃЈ0ЁмtЁм4ЃЉЃЌЕБS=8ЪБЃЌPЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌШ§НЧаЮ
жаЃЌШ§НЧаЮ![]() ЕФШ§ИіЖЅЕуЗжБ№ЪЧ
ЕФШ§ИіЖЅЕуЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЃЈ1ЃЉдкЫљИјЕФЭјИёЭМжаЃЌЛГіетИіЦНУцжБНЧзјБъЯЕЃЛ
ЃЈ2ЃЉЕу![]() ОЙ§ЦНвЦКѓЖдгІЕуЮЊ
ОЙ§ЦНвЦКѓЖдгІЕуЮЊ![]() ЃЌНЋШ§НЧаЮ
ЃЌНЋШ§НЧаЮ![]() зїЭЌбљЕФЦНвЦЕУЕНШ§НЧаЮ
зїЭЌбљЕФЦНвЦЕУЕНШ§НЧаЮ![]() .
.
ЂйЛГіЦНвЦКѓЕФШ§НЧаЮ![]() ЃЛ
ЃЛ
ЂкШє![]() БпЩЯвЛЕу
БпЩЯвЛЕу![]() ОЙ§ЩЯЪіЦНвЦКѓЕФЖдгІЕуЮЊ
ОЙ§ЩЯЪіЦНвЦКѓЕФЖдгІЕуЮЊ![]() ЃЌгУКЌ
ЃЌгУКЌ![]() ЃЌ
ЃЌ![]() ЕФЪНзгБэЪОЕу
ЕФЪНзгБэЪОЕу![]() ЕФзјБъЃЛ(жБНгаДГіНсЙћМДПЩ)
ЕФзјБъЃЛ(жБНгаДГіНсЙћМДПЩ)
ЂлЧѓШ§НЧаЮ![]() ЕФУцЛ§.
ЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЛЈЕъзМБИЙКНјМзЁЂввСНжжЛЈЛмЃЌШєЙКНјМзжжЛЈЛм20ХшЃЌввжжЛЈЛм50ХшЃЌашвЊ900дЊЃЛШєЙКНјМзжжЛЈЛм40ХшЃЌввжжЛЈЛм30ХшЃЌашвЊ960дЊЃЎ
ЃЈ1ЃЉЧѓЙКНјМзЁЂввСНжжЛЈЛмУПХшИїашЖрЩйдЊЃП
ЃЈ2ЃЉИУЛЈЕъЙКНјМзЃЌввСНжжЛЈЛмЙВ100ХшЃЌМзжжЛЈЛмУПХшЪлМл20дЊЃЌввжжЛЈЦыУПХшЪлМл16дЊЃЌЯжИУЛЈЕъАб100ХшЛЈЛмШЋВПЪлГіЃЌШєЛёРћГЌЙ§480дЊЃЌдђжСЩйЙКНјМзжжЛЈЛмЖрЩйХшЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуBЃЌCЕФзјБъЗжБ№ЮЊЃЈ2ЃЌ0ЃЉКЭЃЈ6ЃЌ0ЃЉЃЎ

ЃЈ1ЃЉШЗЖЈAЁЂDЁЂEЁЂFЁЂGЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЫФБпаЮABFGЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌСЌНгBDЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌAEЁЭBDгкEЃЎжБНгаДГіЁЯBAEЕФЖШЪ§ЃЎ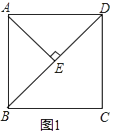
ЃЈ2ЃЉШчЭМ1ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌНЋЁїAEBвдAа§зЊжааФЃЌбиФцЪБеыЗНЯђа§зЊ30ЁуКѓЕУЕНЁїABЁфEЁфЃЌABЁфгыBDНЛгкMЃЌAEЁфЕФбгГЄЯпгыBDНЛгкNЃЎ
ЂйвРЬтвтВЙШЋЭМ1ЃЛ
ЂкгУЕШЪНБэЪОЯпЖЮBMЁЂDNКЭMNжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌEЁЂFЪЧБпBCЁЂCDЩЯЕФЕуЃЌЁїCEFжмГЄЪЧе§ЗНаЮABCDжмГЄЕФвЛАыЃЌAEЁЂAFЗжБ№гыBDНЛгкMЁЂNЃЌаДГіХаЖЯЯпЖЮBMЁЂDNЁЂMNжЎМфЪ§СПЙиЯЕЕФЫМТЗЃЎЃЈВЛБиаДГіЭъећЭЦРэЙ§ГЬЃЉ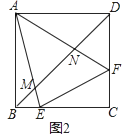
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЯыСЫНтбЇЩњВЮМгПЮЭтЬхг§ЖЭСЖЧщПіЃЌЫцЛњГщШЁБОаЃ40УћбЇЩњНјааЮЪОэЕїВщЃЌЭГМЦећРэВЂЛцжЦСЫШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃК
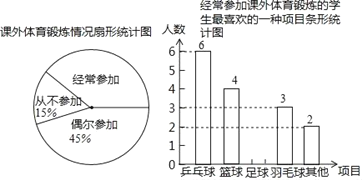
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉПЮЭтЬхг§ЖЭСЖЧщПіЭГМЦЭМжаЃЌЁАОГЃВЮМгЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃЙВга800УћбЇЩњЃЌЧыЙРМЦШЋаЃбЇЩњжаОГЃВЮМгПЮЭтЬхг§ЖЭСЖВЂЯВЛЖЕФЯюФПЪЧЁЁ ЁЁЃЌЦЙХвЧђЕФШЫЪ§гаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=x2Љ2mx+4mЉ8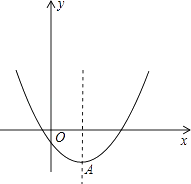
ЃЈ1ЃЉЕБxЁм2ЪБЃЌКЏЪ§жЕyЫцxЕФдіДѓЖјМѕаЁЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉвдХзЮяЯпy=x2Љ2mx+4mЉ8ЕФЖЅЕуAЮЊвЛИіЖЅЕузїИУХзЮяЯпЕФФкНге§Ш§НЧаЮAMNЃЈMЃЌNСНЕудкЮяЯпЩЯЃЉЃЌЧыЮЪЃКЁїAMNЕФУцЛ§ЪЧгыmЮоЙиЕФЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіетИіЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєХзЮяЯпy=x2Љ2mx+4mЉ8гыxжсНЛЕуЕФКсзјБъОљЮЊећЪ§ЃЌЧѓећЪ§mЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉдкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаЃЌвРДЮСЌНгЯТСаИїЕуЃК AЃЈЃ5ЃЌ0ЃЉЃЌBЃЈ1ЃЌ4ЃЉЃЌCЃЈ3ЃЌ3ЃЉЃЌDЃЈ1ЃЌ0ЃЉЃЌEЃЈ3ЃЌЃ3ЃЉЃЌFЃЈ1ЃЌЃ4ЃЉЃЎ

ЃЈ2ЃЉЧыФудкШчЭМЫљЪОЕФЗНИёжНЩЯАДееШчЯТвЊЧѓЩшМЦжБНЧШ§НЧаЮЃК

ЂйЪЙЫќЕФШ§БпжагавЛБпБпГЄВЛЪЧгаРэЪ§ЃЛ
ЂкЪЙЫќЕФШ§БпжагаСНБпБпГЄВЛЪЧгаРэЪ§ЃЛ
ЂлЪЙЫќЕФШ§БпБпГЄЖМВЛЪЧгаРэЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com