
分析 先进行二次根式的化简,再结合二次根式乘除法的运算法则进行求解即可.
解答 解:(1)原式=$\frac{\sqrt{10}}{2}$÷6$\sqrt{7}$×(-5×$\frac{4}{\sqrt{7}}$)
=$\frac{\sqrt{10}}{12\sqrt{7}}$×(-5×$\frac{4}{\sqrt{7}}$)
=-$\frac{20\sqrt{10}}{84}$
=-$\frac{5\sqrt{10}}{21}$.
(2)原式=$\frac{2}{y}$×y2×$\sqrt{xy}$×(-$\frac{3}{2}$x$\sqrt{xy}$)÷$\frac{\sqrt{xy}}{3x}$
=2y$\sqrt{xy}$×(-$\frac{3}{2}$x$\sqrt{xy}$)÷$\frac{\sqrt{xy}}{3x}$
=-3x2y2÷$\frac{\sqrt{xy}}{3x}$
=-9x3y$\sqrt{xy}$.
点评 本题考查了二次根式的乘除法,解答本题的关键在于熟练掌握二次根式的化简及二次根式乘除法的运算法则.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
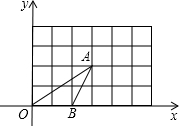 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com