
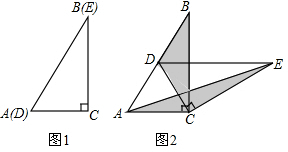
 (1)操作发现
(1)操作发现分析 (1)①如图2,易证△ACD是等边三角形,即可得到∠ACD=∠CDE=60°,由此可得DE∥AC;②易证AD=DC=$\frac{1}{2}$AB,则有AD=BD,从而可得S1=S△ADC.由DE∥AC可得S△ADC=S2,即可得到S1=S2;
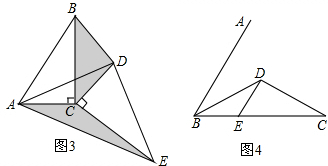
(2)①如图3,作DG⊥BC于点G,作AH⊥CE交EC的延长线于点H,易证△AHC≌△DGC,则有AH=DG,再由CE=CB可得S1=S2;
②如图4①,作DF⊥BD交BA于点F,连接FC,根据①中的结论可得S△DCF=S△BDE,在Rt△BDF中运用三角函数就可求出BF的值;如图4②,延长CD交BA于Q,则∠BQC=90°,作点F关于CQ的对称点F′,显然点F′在BA上,在Rt△BQD中运用三角函数可求出BQ,从而求出FQ(即F′Q)的值,即可得到BF′的值.
解答 解:(1)①DE∥AC.
提示:∵CA=CD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ACD=60°.
∵∠CDE=60°,
∴∠ACD=∠CDE,
∴DE∥AC.
故答案为:平行;
②S1=S2.
理由:∵∠ACB=90°,∠B=30°,∴AC=$\frac{1}{2}$AB.
∵△ACD是等边三角形,∴AD=AC,
∴AD=$\frac{1}{2}$AB,
∴AD=BD,
∴S1=S△ADC.
∵DE∥AC,
∴S△ADC=S2,
∴S1=S2.
故答案为:相等;
(2)①S1=S2仍然成立.
理由:如图3,作DG⊥BC于点G,作AH⊥CE交EC的延长线于点H.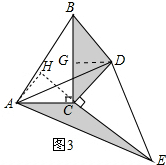
∵∠DCE=∠ACB=90°,
∴∠DCG+∠ACE=180°.
∵∠ACH+∠ACE=180°,
∴∠ACH=∠DCG.
在△AHC和△DGC中,
$\left\{\begin{array}{l}{∠AHC=∠DGC}\\{∠ACH=∠DCG}\\{AC=DC}\end{array}\right.$,
∴△AHC≌△DGC,
∴AH=DG.
∵CE=CB,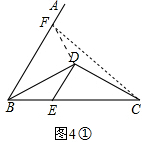
∴S1=S2;
②BF=$\frac{8\sqrt{3}}{3}$或$\frac{4\sqrt{3}}{3}$.
提示:如图4①,作DF⊥BD交BA于点F,连接FC,
根据①中的结论可得S△DCF=S△BDE,
此时,在Rt△BDF中,
$\frac{BD}{BF}$=$\frac{4}{BF}$=cos∠DBF=cos30°=$\frac{\sqrt{3}}{2}$,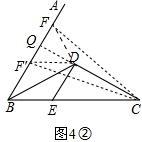
∴BF=$\frac{8\sqrt{3}}{3}$.
如图4②,延长CD交BA于Q,则∠BQC=90°.
作点F关于CQ的对称点F′,显然点F′在BA上,
在Rt△BQD中运用三角函数可求得BQ=2$\sqrt{3}$,
∴F′Q=FQ=BF-BQ=$\frac{2\sqrt{3}}{3}$,
∴BF′=BQ-F′Q=$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查了等边三角形的判定与性质、平行线的判定、全等三角形的判定与性质、三角函数、平行等积法、轴对称性质、30°角所对的直角边等于斜边的一半等知识,通过三角形全等证到CE和BC边上的高相等是解决第(2)①小题的关键;利用(2)①中的结论及轴对称变换是解决第(2)②小题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
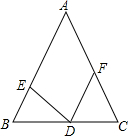 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )| A. | 180°-2∠B | B. | 180°-∠B | C. | ∠B | D. | 90°-∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.0×10-8m | B. | 1.0×10-9m | C. | 1.0×10-10m | D. | 1.0×109m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
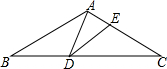 如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.
如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
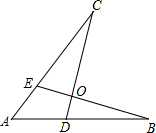 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
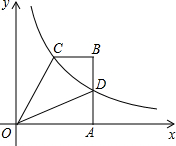 四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.
四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com