
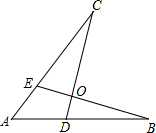
 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.科目:初中数学 来源: 题型:解答题
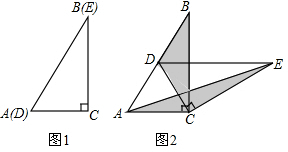
 (1)操作发现
(1)操作发现查看答案和解析>>
科目:初中数学 来源: 题型:选择题
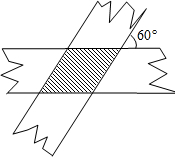 如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )
如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
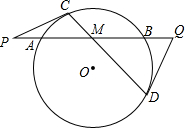 AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:PA=QB.
AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:PA=QB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
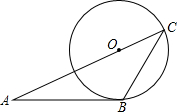 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )| A. | 3π | B. | 4π | C. | 5π | D. | 6π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
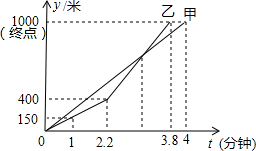 端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com