
分析 先画出图形,再利用中心对称的性质分别得到P1(2,0),点P2(0,-2),P3(-2,0),P4(0,2),P5(2,0),于是这些点的坐标每4个一个循环,而2015=4×503+3,所以点P2015的坐标与点P3的坐标相同,从而得到答案.
解答 解:如图,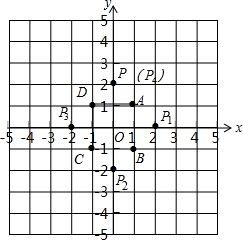
点P1的坐标为(2,0),
点P2的坐标为(0,-2),
点P3的坐标为(-2,0),
点P4的坐标为(0,2),
点P5的坐标为(2,0),
而2015=4×503+3,
所以点P2015的坐标与点P3的坐标相同,为(-2,0).
故答案为(-2,0).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了对称变换.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
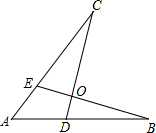 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$mm2 | B. | $\frac{3\sqrt{3}}{2}$mm2 | C. | 3$\sqrt{3}$mm2 | D. | 6$\sqrt{3}$mm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
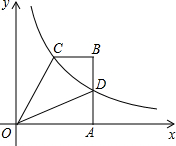 四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.
四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com