
如图,△ABC中,AD是边BC上的中线,过点A作AE//BC,过点D作DE//AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.

(1)证明见解析
(2)证明见解析
【解析】
试题分析:(1)由AE//BC,DE//AB可知四边形ABDE是平行四边形,从而可得AE平行且等于BD,再由BD=CD,由此可得AE平行且等于CD,可得到四边形ADCE是平行四边形,所以得到AD=EC
(2)由∠BAC=Rt∠,AD是边BC上的中线可得AD=CD,再由(1)可得四边形ADCE是菱形
试题解析:(1)∵AE//BC,DE//AB
∴四边形ABDE是平行四边形
∴AE=BD,AE//BD
又BD=CD
∴AE=CD,AE//CD
∴四边形ADCE是平行四边形
∴AD=CE
∵∠BAC=Rt∠,AD是边BC上的中线
∴AD=CD
又∵四边形ADCE是平行四边形
∴平行四边形ADCE是菱形
考点:1、平行四边形的性质与判定;2、直角三角形的性质;3、菱形的判定


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届江苏省八年级下学期期中联考数学试卷(解析版) 题型:解答题
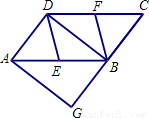
如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:解答题
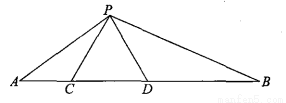
如图,在△PAB中,点C、D在边AB上,PC=PD=CD,∠APB=120°.
(1)试说明△APC与△PBD相似.
(2)若CD=1,AC=x,BD=y,请你求出y与x之间的函数关系式.
(3)小明猜想:若PC=PD=1,∠CPD=α,∠APB=β,只要α与β之间满足某种关系式,问题(2)中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出α与β所满足的关系式;若不同意,请说明理曲.
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:填空题
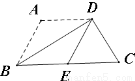
在梯形ABCD中,AD∥BC,AB=DC=3,沿对角线BD翻折梯形ABCD,若点A恰好落在下底BC的中点E处,则该梯形的面积为 .
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为( )
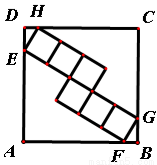
A.6 B.5 C.2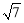 D.
D.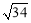
查看答案和解析>>
科目:初中数学 来源:2015届江苏省盐城市东台市八年级下学期第一次月考数学试卷(解析版) 题型:填空题
下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为 .
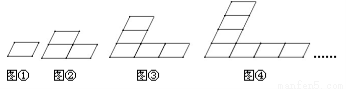
查看答案和解析>>
科目:初中数学 来源:2015届江苏省泰州市姜堰区八年级下学期期末考试数学试卷(解析版) 题型:选择题
在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是
A.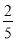 B.
B.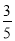 C.
C.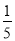 D.
D.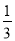
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com