
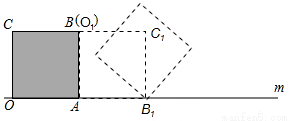
把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为 ,经过61次旋转后,顶点O经过的总路程为 .
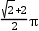 ,
,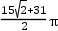
【解析】为了便于标注字母,且更清晰的观察,每次旋转后向右稍微平移一点,作出前几次旋转后的图形,点O的第1次旋转路线是以正方形的边长为半径,以90°为圆心角的扇形,第2次旋转路线是以正方形的对角线长为半径,以90°为圆心角的扇形,第3次旋转路线是以正方形的边长为半径,以90°为圆心角的扇形,第4次旋转点O没有移动,旋转后与最初正方形的放置相同.
①根据弧长公式列式进行计算即可得解;
②求出61次旋转中有几个4次,然后根据以上的结论进行计算即可求解.
【解析】
如图,为了便于标注字母,且位置更清晰,每次旋转后不防向右移动一点,
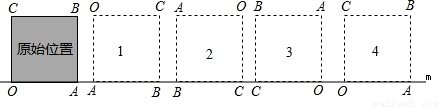
第1次旋转路线是以正方形的边长为半径,以90°为圆心角的扇形,路线长为 =
=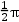 ;第2次旋转路线是以正方形的对角线长
;第2次旋转路线是以正方形的对角线长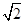 为半径,以90°为圆心角的扇形,路线长为
为半径,以90°为圆心角的扇形,路线长为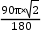 =
= ;第3次旋转路线是以正方形的边长为半径,以90°为圆心角的扇形,路线长为
;第3次旋转路线是以正方形的边长为半径,以90°为圆心角的扇形,路线长为 =
=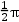 ;第4次旋转点O没有移动,旋转后与最初正方形的放置相同,因此4次旋转,顶点O经过的路线长为
;第4次旋转点O没有移动,旋转后与最初正方形的放置相同,因此4次旋转,顶点O经过的路线长为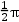 +
+ +
+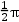 =
=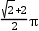 ;∵61÷4=15…1,∴经过61次旋转,顶点O经过的路程是4次旋转路程的15倍加上第1次路线长,
;∵61÷4=15…1,∴经过61次旋转,顶点O经过的路程是4次旋转路程的15倍加上第1次路线长,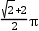 ×15+
×15+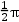 =
=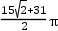 .
.
故答案分别是: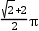 ;
;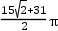 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014中考名师推荐数学模型思想(解析版) 题型:选择题
现有球迷150人欲同时租用A、B、C三种型号客车去观看世界杯足球赛,其中A、B、C三种型号客车载容量分别为50人、30人、10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有( )
A.3种 B.4种 C.5种 D.6种
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学实数(解析版) 题型:填空题
将1、 、
、 、
、 按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(7,3)所表示的数是 ;(5,2)与(20,17)表示的两数之积是 .
按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(7,3)所表示的数是 ;(5,2)与(20,17)表示的两数之积是 .

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )

A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
已知⊙O1的半径是3cm,⊙O2的半径是2cm,O1O2= cm,则两圆的位置关系是( )
cm,则两圆的位置关系是( )
A.相离
B.外切
C.相交
D.内切
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:填空题
如图,O为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为________.
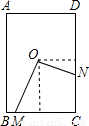
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
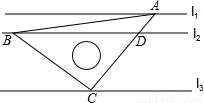
直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A.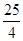 B.
B. C.
C.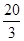 D.
D.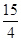
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数(解析版) 题型:解答题
某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
销售单价x (元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y (件) | … | 450 | 400 | 300 | 250 | … |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com