
现有球迷150人欲同时租用A、B、C三种型号客车去观看世界杯足球赛,其中A、B、C三种型号客车载容量分别为50人、30人、10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有( )
A.3种 B.4种 C.5种 D.6种
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:选择题
下列事件中,必然事件是 ( )
A.掷一枚硬币,正面朝上.
B.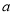 是有理数,则
是有理数,则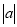 ≥0.
≥0.
C.某运动员跳高的最好成绩是20 .1米.
D.从车间刚生产的产品中任意抽取一个,是次品.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学解直角三角形(解析版) 题型:填空题
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为____________.

本题主要是考查切线的性质及解直角三角形的应用,关键是利用平行把已知角代换成其它相等的容易求出其正切值的角.可以通过证明∠EFO=∠HDE,再求出∠HDE的正切值就是∠EFO的正切值.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学点、线、面、角(解析版) 题型:选择题
如图,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )

①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学整式(解析版) 题型:选择题
纳米是非常小的长度单位,已知1纳米= 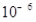 毫米,某种病毒的直径为100纳米,若将这种病毒排成1毫米长,则病毒的个数是( )
毫米,某种病毒的直径为100纳米,若将这种病毒排成1毫米长,则病毒的个数是( )
A.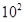 个 B.
个 B.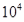 个
个
C.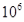 个 D.
个 D.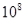 个
个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )
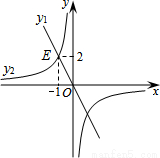
A.
B.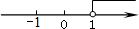
C.
D.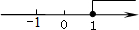
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的规律(解析版) 题型:填空题
把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为 ,经过61次旋转后,顶点O经过的总路程为 .
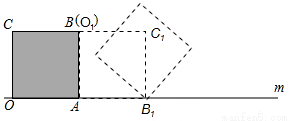
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com