
ЁОЬтФПЁПЮЪЬтдаЭЃКдкЭМЂйЕФОиаЮMNPQжаЃЌЕуEЁЂFЁЂGЁЂHЗжБ№дкNPЁЂPQЁЂQMЁЂMNЩЯЃЌШєЁЯ1=ЁЯ2=ЁЯ3=ЁЯ4ЃЌдђГЦЫФБпаЮEFGHЮЊОиаЮMNPQЕФЗДЩфЫФБпаЮЃЎ
ВйзїгыЬНОПЃКдкЭМЂкЃЌЭМЂлЕФОиаЮABCDжаЃЌAB=4ЃЌBC=8ЕуEЁЂFЗжБ№дкBCЁЂCDБпЩЯЃЌЪдРћгУе§ЗНаЮЭјИёЗжБ№зїГіСНЭМжаОиаЮABCDЕФЗДЩфЫФБпаЮEFGHЃЌВЂЧѓГіУПИіЗДЩфЫФБпаЮEFGHЕФжмГЄЃЎ
ЗЂЯжгыгІгУЃКгЩЧАУцЕФВйзїПЩвдЗЂЯжвЛИіОиаЮгаВЛЭЌЕФЗДЩфЫФБпаЮЃЌЧветаЉЗДЩфЫФБпаЮЕФжмГЄЖМЯрЕШЃЌШєдкЭМЂйОиаЮMNPQжаЃЌMN=3ЃЌNP=4дђЦфЗДЩфЫФБпаЮEFGHЕФжмГЄЮЊЁЁЁЁЃЎ

ЁОД№АИЁП(1)МћНтЮіЃЛЃЈ2ЃЉ8![]() ЃЛЃЈ3ЃЉ10
ЃЛЃЈ3ЃЉ10
ЁОНтЮіЁП
(1)ЁЂИљОнЗДЩфЫФБпаЮЕФКЌвхКЭEЁЂFЕуЕФЮЛжУЛГіМДПЩЃЛ(2)ЁЂИљОнЙДЙЩЖЈРэЧѓГіБпГЄЃЌМДПЩЧѓГіжмГЄЃЛ(3)ЁЂбгГЄGHНЛPNЕФбгГЄЯпгкЕуAЃЌЙ§ЕуGзїGKЁЭNPгкKЃЌжЄУїRtЁїFPEКЭRtЁїFPBШЋЕШЃЌДгЖјЧѓГіGBЕФГЄЖШЃЌИљОнЫФБпаЮжмГЄЕШгк2GBЕУГіД№АИЃЎ
ЃЈ1ЃЉзїЭМШчЯТЃК
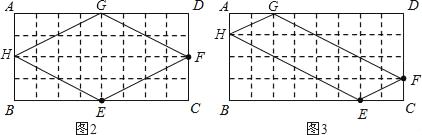
ЃЈ2ЃЉдкЭМ2жаЃЌEF=FG=GH=HE=![]() =2
=2![]() ЃЌЁрЫФБпаЮEFGHЕФжмГЄЮЊ4ЁС2
ЃЌЁрЫФБпаЮEFGHЕФжмГЄЮЊ4ЁС2![]() =8
=8![]() ЃЌ
ЃЌ
дкЭМ3жаЃЌEF=GH=![]() ЃЌFG=HE=
ЃЌFG=HE=![]() =3
=3![]() ЃЌ
ЃЌ
ЁрЫФБпаЮEFGHЕФжмГЄЮЊ2ЁС![]() +2ЁС3
+2ЁС3![]() =2
=2![]() +6
+6![]() =8
=8![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ4ЃЌбгГЄGHНЛPNЕФбгГЄЯпгкЕуAЃЌЙ§ЕуGзїGKЁЭNPгкKЃЌ
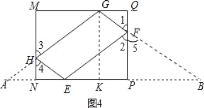
ЁпЁЯ1=ЁЯ2ЃЌЁЯ1=ЁЯ5ЃЌЁрЁЯ2=ЁЯ5ЃЎ
дкЁїFPEКЭЁїFPBжаЃЌ ЃЌЁрRtЁїFPEЁеRtЁїFPBЃЈASAЃЉЃЌЁрEF=BFЃЌEP=PBЃЌ
ЃЌЁрRtЁїFPEЁеRtЁїFPBЃЈASAЃЉЃЌЁрEF=BFЃЌEP=PBЃЌ
ЭЌРэЃКAH=EHЃЌNA=ENЃЎЁрAB=2NP=8ЃЎЁпЁЯB=90ЁуЉЁЯ5=90ЁуЉЁЯ1ЃЌЁЯA=90ЁуЉЁЯ3ЃЌ
ЁрЁЯA=ЁЯBЃЎЁрGA=GBЃЎдђKB=![]() AB=4ЃЌЁрGB=
AB=4ЃЌЁрGB=![]() =5ЃЌ
=5ЃЌ
ЁрЫФБпаЮEFGHЕФжмГЄЮЊЃК2GB=10ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє x Тњзу (9x)(x4)=4ЃЌ Чѓ (4x)2+(x9)2 ЕФжЕ.
Щш 9x=aЃЌx4=bЃЌ дђ (9x)(x4)=ab=4ЃЌa+b=(9x)+(x4)=5 ЃЌ
Ёр(9x)2+(x4)2=a2+b2=(a+b)22ab=522ЁС4=13
ЧыЗТееЩЯУцЕФЗНЗЈЧѓНтЯТУцЮЪЬтЃК
(1)Шє x Тњзу (5x)(x2)=2ЃЌ Чѓ (5x)2+(x2)2 ЕФжЕ
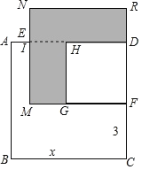
(2)вбжЊе§ЗНаЮ ABCD ЕФБпГЄЮЊ x ЃЌ E ЃЌ F ЗжБ№ЪЧ AD ЁЂ DC ЩЯЕФЕуЃЌЧв AE=1 ЃЌ CF=3 ЃЌГЄЗНаЮ EMFD ЕФУцЛ§ЪЧ 48 ЃЌЗжБ№вд MF ЁЂ DF зїе§ЗНаЮЃЌЧѓвѕгАВПЗжЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуFдкADЩЯЃЌЕуEдкBCЩЯЃЌАбетИіОиаЮбиEFелЕўКѓЃЌЪЙЕуDЧЁКУТфдкBCБпЩЯЕФGЕуДІЃЌШєОиаЮУцЛ§ЮЊ![]() ЧвЁЯAFG=60ЁуЃЌGE=2BGЃЌдђелКлEFЕФГЄЮЊЃЈ ЃЉ
ЧвЁЯAFG=60ЁуЃЌGE=2BGЃЌдђелКлEFЕФГЄЮЊЃЈ ЃЉ
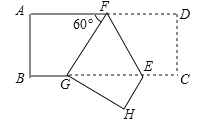
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
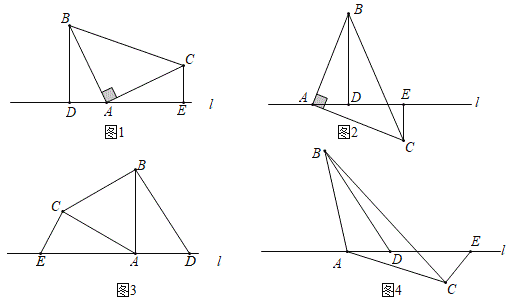
ЁОЬтФПЁПЃЈ1ЃЉвбжЊ![]() ЪЧжБНЧШ§НЧаЮЃЌ
ЪЧжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯпlОЙ§Еу
ЃЌжБЯпlОЙ§Еу![]() ЃЌЗжБ№ДгЕу
ЃЌЗжБ№ДгЕу![]() ЁЂ
ЁЂ![]() ЯђжБЯпlзїДЙЯпЃЌДЙзуЗжБ№ЮЊ
ЯђжБЯпlзїДЙЯпЃЌДЙзуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЎЕБЕу
ЃЎЕБЕу![]() ЃЌ
ЃЌ![]() ЮЛгкжБЯпlЕФЭЌВрЪБЃЈШчЭМ
ЮЛгкжБЯпlЕФЭЌВрЪБЃЈШчЭМ![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЎШчЭМ2ЃЌШєЕу
ЃЎШчЭМ2ЃЌШєЕу![]() дкжБЯпlЕФвьВрЃЌЦфЫќЬѕМўВЛБфЃЌ
дкжБЯпlЕФвьВрЃЌЦфЫќЬѕМўВЛБфЃЌ![]() ЪЧЗёвРШЛГЩСЂЃПШєГЩСЂЃЌЧыаДГіжЄУїЙ§ГЬЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёвРШЛГЩСЂЃПШєГЩСЂЃЌЧыаДГіжЄУїЙ§ГЬЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉБфЪНвЛЃКШчЭМ3ЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌжБЯпlОЙ§Еу
ЃЌжБЯпlОЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дкжБЯпlЩЯЃЌЕу
ЗжБ№дкжБЯпlЩЯЃЌЕу![]() ЁЂ
ЁЂ![]() ЮЛгкlЕФЭЌвЛВрЃЌШчЙћ
ЮЛгкlЕФЭЌвЛВрЃЌШчЙћ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ЃЈ3ЃЉБфЪНЖўЃКШчЭМ4ЃЌ![]() жаЃЌвРШЛга
жаЃЌвРШЛга![]() ЃЌШєЕу
ЃЌШєЕу![]() ЃЌ
ЃЌ![]() ЮЛгкlЕФСНВрЃЌШчЙћ
ЮЛгкlЕФСНВрЃЌШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКМзЁЂввСНГЕЗжБ№ДгЯрОр300kmЕФA,BСНЕиЭЌЪБГіЗЂЯрЯђЖјааЃЌМзЕНBЕиКѓСЂМДЗЕЛиЃЌЯТЭМЪЧЫќУЧРыИїздГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЭМЯѓ.
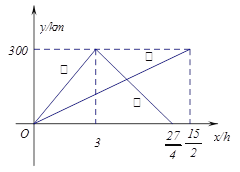
ЃЈ1ЃЉЧѓМзГЕРыГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂБъУїздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєвбжЊввГЕааЪЛЕФЫйЖШЪЧ40ЧЇУз/аЁЪБЃЌЧѓГіЗЂКѓЖрГЄЪБМфЃЌСНГЕРыИїздГіЗЂЕиЕФОрРыЯрЕШЃЛ
ЃЈ3ЃЉЫќУЧдкааЪЛЙ§ГЬжагаМИДЮЯргі.ВЂЧѓГіУПДЮЯргіЕФЪБМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
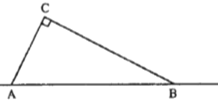
ЁОЬтФПЁПШчЭМЃЌ![]() ЮЊвЛЬѕЙЋТЗЃЌЯжгавЛДІ
ЮЊвЛЬѕЙЋТЗЃЌЯжгавЛДІ![]() ашвЊБЌЦЦЃЌБЌЦЦЕу
ашвЊБЌЦЦЃЌБЌЦЦЕу![]() жмЮЇ
жмЮЇ![]() ЗЖЮЇФкгаЮЃЯеЃЌвбжЊЕу
ЗЖЮЇФкгаЮЃЯеЃЌвбжЊЕу![]() гыЙЋТЗЩЯЕФЭЃППеО
гыЙЋТЗЩЯЕФЭЃППеО![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌгыЭЃППеО
ЃЌгыЭЃППеО![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
(1)ЭЈЙ§МЦЫуЫЕУїЙЋТЗ![]() ЖЮЪЧЗёДцдкЮЃЯеЃЛ
ЖЮЪЧЗёДцдкЮЃЯеЃЛ
(2)жБНгаДГіЙЋТЗ![]() ДцдкЮЃЯеЕФТЗЖЮГЄЖШ.
ДцдкЮЃЯеЕФТЗЖЮГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбОиаЮжНЦЌABCDбиЖдНЧЯпелЕўЃЌЩшжиЕўВПЗжЮЊЁїEBDЃЌФЧУДЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ

A. ЁїEBDЪЧЕШбќШ§НЧаЮЃЌEB=ED B. елЕўКѓЁЯABEКЭЁЯCЁфBDвЛЖЈЯрЕШ
C. елЕўКѓЕУЕНЕФЭМаЮЪЧжсЖдГЦЭМаЮ D. ЁїEBAКЭЁїEDCЁфвЛЖЈЪЧШЋЕШШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВйзїЗЂЯжЃКШчЭМЃЌвбжЊЁїABCКЭЁїADEОљЮЊЕШбќШ§НЧаЮЃЌABЃНACЃЌADЃНAEЃЌНЋетСНИіШ§НЧаЮЗХжУдквЛЦ№ЃЌЪЙЕуBЃЌDЃЌEдкЭЌвЛжБЯпЩЯЃЌСЌНгCEЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯABCЃНЁЯACBЃНЁЯADEЃНЁЯAEDЃН55ЁуЃЌЧѓжЄЃКЁїBADЁеЁїCAEЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЧѓЁЯBECЕФЖШЪ§ЃЛ
ЭиЙуЬНЫїЃКЃЈ3ЃЉШчЭМ2ЃЌШєЁЯCABЃНЁЯEADЃН120ЁуЃЌBDЃН4ЃЌCFЮЊЁїBCEжаBEБпЩЯЕФИпЃЌЧыжБНгаДГіEFЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшaЃЌbЃЌcЪЧЁїABCЕФШ§ЬѕБпЃЌЙигкxЕФЗНГЬ![]() x2+
x2+![]() x+c-
x+c-![]() a=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЗНГЬ3cx+2b=2aЕФИљЮЊx=0.
a=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЗНГЬ3cx+2b=2aЕФИљЮЊx=0.
ЃЈ1ЃЉЪдХаЖЯЁїABCЕФаЮзДЃЛ
ЃЈ2ЃЉШєaЃЌbЮЊЗНГЬx2+mx-3m=0ЕФСНИіИљЃЌЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com