
����Ŀ����ͼ��������y=ax2��2ax��4��x����������ڵ�A����y���ڵ�B����OA=OB��
��1����������ߵĽ���ʽ��
��2������MΪAB���е�,�ҡ�PMQ=45�㣬��PMQ��AB��ͬ��,�Ե�MΪ��ת���Ľ���PMQ��ת,MP��y���ڵ�C��MQ��x���ڵ�D.��AD=m(m��0)��BC=n����n��m֮��ĺ�����ϵʽ��
��3���ڣ�2����������,����PMQ��һ��ǡ�þ�������������x�����һ������ʱ,ֱ��д����PMQ����һ����x��Ľ������꣮

���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��![]()
�������������������1����������![]() ��B��0��-4�����ٽ��OA��OB���ҵ�A��x���������ϣ�������õ�A�����꣬�Ӷ���ý����
��B��0��-4�����ٽ��OA��OB���ҵ�A��x���������ϣ�������õ�A�����꣬�Ӷ���ý����
��2���ȸ��ݵ���ֱ�������ε����ʵõ���OAB����OBA��45����AB=![]() ��������ADM+��AMD��135��������CMD��45���ɵ���AMD+��BMC��135����֤����ADM�ס�BMC���������������ε����ʿɵ�
��������ADM+��AMD��135��������CMD��45���ɵ���AMD+��BMC��135����֤����ADM�ס�BMC���������������ε����ʿɵ�![]() ���ٸ���MΪAB���е�ɵ�AM��BM��
���ٸ���MΪAB���е�ɵ�AM��BM��![]() �������������ĺ�����ϵʽ��
�������������ĺ�����ϵʽ��
��3����![]() �������������
�������������![]() ��x����һ������Ϊ���ɵ�A��B����������AB�е�M�����꣬�ٷ�����MP�����㣨-2��0��ʱ������MQ�����㣨-2��0��ʱ�������������⼴��.
��x����һ������Ϊ���ɵ�A��B����������AB�е�M�����꣬�ٷ�����MP�����㣨-2��0��ʱ������MQ�����㣨-2��0��ʱ�������������⼴��.
��1����������![]() ��B��0��-4����
��B��0��-4����
��OA��OB���ҵ�A��x���������ϣ�
��A��4��0��
��A��4��0������![]() ��
��
![]() �����
�����![]()
�������ߵĽ���ʽΪ![]() ��
��
��2����OA��OB=4����AOB��90����
���OAB����OBA��45����AB=![]() ��
��
���ADM+��AMD��135��
�ߡ�CMD��45��
���AMD+��BMC��135����
���ADM����BMC��
���ADM�ס�BMC��
��![]() ����
����![]() ��
��
��MΪAB���е㣬
��AM��BM��![]() ��
��
��![]() ��������ĺ�����ϵʽ��
��������ĺ�����ϵʽ��
��3����![]()
��������![]() ��x����һ������Ϊ��-2��0����
��x����һ������Ϊ��-2��0����
��A��4��0����B��0��-4����
��AB�е�M������Ϊ��2��-2��
����MP�����㣨-2��0��ʱ��MP�Ľ���ʽΪ![]()
��MP��y���ڵ�C��
��C��0��-1������n=BC��OB��OC��3
��![]() ����
����![]()
��OD=OA-AD=![]() ����D��
����D��![]() ��0��
��0��
��MQ����M��2��-2����D��![]() ��0����
��0����
��MQ�Ľ���ʽΪ![]() ��
��
����MQ�����㣨-2��0��ʱ��MQ�Ľ���ʽΪ![]()
��ʱ����D������Ϊ��-2��0����m=AD=6
��![]() ����BC��
����BC��![]()
��OC��OB��BC��![]() ����C��0����
����C��0���� ![]() ��
��
��MP����M��2��-2����C��0���� ![]() ����
����
��MP�Ľ���ʽΪ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�˽�ij�������꼶ѧ����������������������ȡ150��ѧ����������Ϊһ�����������߾���141cm��175cm֮�䣨ȡ�������ף���������ֳ�7�飬���Ƴ�Ƶ���ֲ�ֱ��ͼ(������)������ͼ���ṩ����Ϣ������������⣺
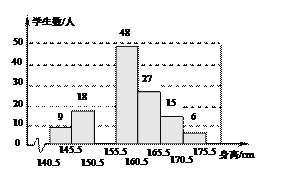
(1) ��ȫƵ���ֲ�ֱ��ͼ��
(2) ��ȡ�������У�ѧ�����ߵ���λ�����ĸ�С��?
(3) �õ�������3 000�����꼶ѧ���������������߲�����161cm��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУΪ�˽������������ҵ�����ƻ�����һ��ƽ����Ժ�һ��ѧϰ������Ͷ��������1̨ƽ�����3 000Ԫ������1̨ѧϰ��800Ԫ.
(1)ѧУ����ʵ���������������ƽ����Ժ�ѧϰ����100̨��Ҫ������ܷ��ò�����168 000Ԫ������ƽ�����������̨��
(2)��(1)��������������ѧϰ����̨��������ƽ�����̨����1.7��.�������ļ��ֹ��������ַ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ˮ�����¼ƵĶ���y���棩��ˮ�����ij���x��cm��֮����һ�κ�����ϵ������һ֧ˮ�����¼ƣ��䲿�̶ֿ��߲���������ͼ�������м�¼���Ǹ����¼Ʋ��������̶������Ӧˮ�����ij��ȣ� ![]()
ˮ�����ij���x��cm�� | 4.0 | �� | 8.0 | 9.6 |
���¼ƵĶ���y���棩 | 35.0 | �� | 40.0 | 42.0 |
��1����y����x�ĺ�����ϵʽ������Ҫд�������Ա���x��ȡֵ��Χ����
��2���ø����¼Ʋ�����ʱ��ˮ�����ij���Ϊ6.0cm�����ʱ���¼ƵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ� ����
A.���е��������ζ�����B.���߳ɱ�����������������������
C.��һ������ȵ�������������������D.��һ������100����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����գ�

(1)��ֱ��ED��BC��ֱ��AB���أ����1��__________��ͬλ��.
(2)��ֱ��ED��BC��ֱ��AF���أ����3��__________���ڴ���.
(3)��1�͡�3��ֱ��AB��AF��ֱ��__________���ع��ɵ�__________��.
(4)��2�͡�4��ֱ��__________��__________��ֱ��BC���ع��ɵ�__________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+2bx+c��b��cΪ��������
����b=1��c=��3ʱ������κ����ک�2��x��2�ϵ���Сֵ��
����c=3ʱ������κ�����0��x��4�ϵ���Сֵ��
����c=4b2ʱ�������Ա���x��ֵ����2b��x��2b+3������£������Ӧ�ĺ���ֵy����СֵΪ21�����ʱ���κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P��m��3��4��2m���������ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com