
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,我们把这条封闭曲线称为“蛋线”,已知点C的坐标为(0,- ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限内是否存在一点P,使得∆PBC的面积最大?若存在,求出∆PBC面积的最大值;若不存在,请说明理由;
(3)当∆BDM为直角三角形时,请直接写出m的值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M、N两点间的距离为MN= .
.
(1)A(-1,0),B(3,0);(2)存在, ;(3)-1或-
;(3)-1或- .
.
解析试题分析:(1)将y=mx2-2mx-3m化为交点式,即可得到A、B两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到△PBC面积的最大值;
(3)先表示出DM2,BD2,MB2,再分两种情况:①DM2+BD2=MB2时;②DM2+MB2=BD2时,讨论即可求得m的值.
试题解析:(1)y=mx2-2mx-3m=m(x-3)(x+1),
∵m≠0,
∴当y=0时,x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得: ,解得
,解得 ,
,
故C1:y= x2-x-
x2-x- .
.
依题意,设点P的坐标为(n, n2-n-
n2-n- )(0<n<3)
)(0<n<3)
则S∆PBC=S∆POC+S∆BOP-S∆BOC = ×
× ×n+
×n+ ×3×(-
×3×(- n2+n+
n2+n+ )-
)- ×3×
×3×
=- (n-
(n- )2+
)2+
∵- <0,
<0,
∴当n= 时S∆PBC的最大值是
时S∆PBC的最大值是
(3)y=mx2-2mx-3m=m(x-1)2-4m,顶点M坐标(1,-4m),
当x=0时,y=-3m,
∴D(0,-3m),B(3,0),
∴DM2=(0-1)2+(-3m+4m)2=m2+1,
MB2=(3-1)2+(0+4m)2=16m2+4,
BD2=(3-0)2+(0+3m)2=9m2+9,
当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.
①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,
解得m=-1(∵m<0,∴m=1舍去);
②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,
解得m=- (m=
(m= 舍去).
舍去).
综上,m=-1或- 时,△BDM为直角三角形.
时,△BDM为直角三角形.
考点: 二次函数综合题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
平面直角坐标系中,抛物线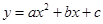 交
交 轴于A、B两点(点A在点B左侧),与
轴于A、B两点(点A在点B左侧),与 轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线
轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线 交
交 轴于点E,点D为顶点.
轴于点E,点D为顶点.
(1)求抛物线的解析式;
(2)点P是直线AC下方的抛物线上一点,且 ,,求点P的坐标;
,,求点P的坐标;
(3)点M是第一象限内抛物线上一点,且∠MAC=∠ADE,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为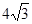 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.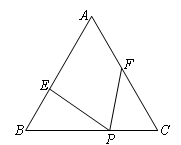
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.
(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=- x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。
的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。
⑴求这个二次函数的表达式;
⑵连结PO、PC,在同一平面内把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由;
⑶当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com