
【题目】如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上一个动点(点A与点B不重合),在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C,连接OC、CD.设点A的横坐标为t.
(1)用含t的式子表示点E的坐标为 ;
(2)当t为何值时,∠OCD=180°?
(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.
【答案】
(1)(t+4,8)
(2)
【解答】解:
如图所示;过点D作DH⊥OF,垂足为H.

∵AC⊥OA,
∴∠OAC=90°.
∴∠BAO+∠EAC=90°.
又∵∠BOA+∠BAO=90°,
∴∠EAC=∠BOA.
又∵∠OBA=∠AEC,
∴△OBA∽△AEC.
∴![]() ,即
,即![]() .
.
∴EC=![]() .
.
∴点C的坐标为(t+4,8﹣![]() )
)
∵∠OCD=180°,
∴点C在OD上.
∵CF∥DH,
∴![]() ,即
,即![]()
解得:![]() ,
,![]() (舍去).
(舍去).
所以当t=4![]() ﹣4时,∠OCD=180°.
﹣4时,∠OCD=180°.
(3)
当0<t<16时,三角形OCF的面积=![]() ×OFFC=
×OFFC=![]() (t+4)(8-
(t+4)(8-![]() t)=
t)=![]() ,
,
当t>16时,三角形OCF的面积=![]() ×OFFC=
×OFFC=![]() (t+4)(
(t+4)(![]() t﹣8)=
t﹣8)=![]() ,
,
∴s与t的函数关系式为s= .
.
【解析】(1)由点B坐标为(0,8),可知OB=8,根据线段垂直平分线的定义可知:AE=4,从而求得:BE=t+4,故此点E的坐标为(t+4,8);
(2)过点D作DH⊥OF,垂足为H.先证明△OBA∽△AEC,由相似三角形的性质可知![]() ,可求得EC=
,可求得EC=![]() ,从而得到点C的坐标为(t+4,8﹣
,从而得到点C的坐标为(t+4,8﹣![]() ),因为∠OCD=180°,CF∥DH,可知
),因为∠OCD=180°,CF∥DH,可知![]() ,即
,即![]() 从而可解得t的值;
从而可解得t的值;
(3)三角形OCF的面积=![]() ×OFFC , 从而可得S与t的函数关系式.
×OFFC , 从而可得S与t的函数关系式.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们有吃粽子的习惯.某校数学兴趣小组为了了解本校学生喜爱粽子的情况,随机抽取了50名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图(注:每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角为 ;条形统计图中,喜欢“糖馅”粽子的人数为 ;
(2)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和;
(3)小军最爱吃肉馅粽子,小丽最爱吃糖馅粽子.某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只,让小军、小丽每人各选一只.请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC.
(1)求证:AC是⊙O的切线;
(2)若BD=OB=4,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′B′C,点A′恰好落在AC上,连接CC′,则∠ACC′= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y= ![]() ,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 .
,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
A.7
B.11
C.13
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E. 
(1)求证:∠BDC=∠A;
(2)若CE=2 ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
(3)在(2)的条件下,求弧BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E. 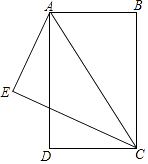
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com