
【题目】推理填空,如图,已知∠A=∠F,∠C=∠D,试说明 BD∥CE.

解:∵∠A=∠F(已知),
∴ ∥ ( ),
∴∠D+∠DBC=180°( ),
又∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴BD∥CE( )
【答案】AC;DF;内错角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补、两直线平行.
【解析】
由已知内错角相等,利用内错角相等两直线平行得到DF与AC平行,再利用两直线平行同旁内角互补,得到一组等量关系,与已知角等量代换得到一对同旁内角互补,利用同旁内角互补两直线平行即可得证
解:解:∵∠A=∠F(已知),
∴AC∥DF(内错角相等,两直线平行),
∴∠D+∠DBC=180°(两直线平行,同旁内角互补 ),
又∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴BD∥CE(同旁内角互补、两直线平行)
故答案为:AC;DF;内错角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补、两直线平行.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,两根长度为12米的绳子,一端系在旗杆上的同一位置A点,另一端分别固定在地面上的两个木桩B,C上(绳结处的误差忽略不计),现在只有一把卷尺,如何检验旗杆是否垂直于地面BC?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.
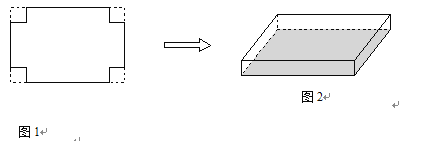
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线![]() ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, ![]() (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
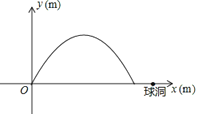
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:如图1,在![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() ;
;
发现:直角三角形中,如果有一个锐角等于![]() ,那么这个角所对的直角边等于斜边的_______.
,那么这个角所对的直角边等于斜边的_______.
应用:如图2,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决下列两个问题:

(1)如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;
解:PA+PB的最小值为 .
(2)如图2.点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若![]() ,则
,则![]() ;②直角三角形的两个锐角互余:③如果
;②直角三角形的两个锐角互余:③如果![]() ,那么
,那么![]() ④
④![]() 个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com