
【题目】(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线![]() ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, ![]() (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
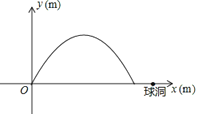
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
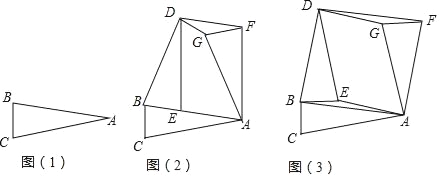
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,(一张铁皮只能生产一种产品)
(1)向用多少张铁皮做盒身,多少张铁皮做盒底,可以正好用完190张铁皮并制成一批完整的盒子?
(2)这批盒子一共有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空,如图,已知∠A=∠F,∠C=∠D,试说明 BD∥CE.

解:∵∠A=∠F(已知),
∴ ∥ ( ),
∴∠D+∠DBC=180°( ),
又∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴BD∥CE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m,台阶AC的坡度为1∶![]() ,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
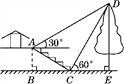
A. 6 m B. 7 m C. 8 m D. 9 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
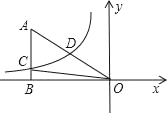
A. 12 B. 9 C. 6 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com