
【题目】如图所示,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:
,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:![]() .
.

【答案】详见解析
【解析】
∠ADC和∠BDE所在的三角形肯定不全等,那么本题需要作辅助线.△ABC是等腰直角三角形,常用的辅助线是作三线里面的一线.可发现要证全等,已包含两个条件需利用全等得到另一边对应相等.
证明:如图: 作CH⊥AB于H交AD于P,

∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∴∠HCB=90°-∠CBA=45°=∠CBA=45°.
又∵BC中点为D,
∴CD=BD.
又CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90°,∠PCO+∠CPO=90°,∠APH=∠CPO
∴∠PAH=∠ECH,
在△APH与△CEH中有:
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又PC=CH-PH,BE=BH-HE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45°,即∠EBD=45°,CH⊥AB,
∴∠PCD=45°=∠EBD,
在△PDC与△EDB中有:
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠EDB.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线![]() ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, ![]() (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
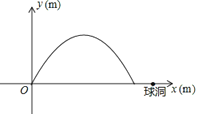
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边三角形ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.

(1)连接AQ、CP交于点M,则在P,Q运动的过程中,证明![]() ≌
≌![]() ;
;
(2)![]() 会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)P、Q运动几秒时,![]() 是直角三角形?
是直角三角形?
(4)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则![]() 变化吗?若变化说明理由,若不变,则求出它的度数。
变化吗?若变化说明理由,若不变,则求出它的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备添置一批计算机.
方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为![]() 、
、![]() 元.
元.
![]() 分别写出
分别写出![]() 、
、![]() 的函数关系式;
的函数关系式;
![]() 当学校添置多少台计算机时,两种方案的费用相同?
当学校添置多少台计算机时,两种方案的费用相同?
![]() 采用哪一种方案较省钱?说说你的理由.
采用哪一种方案较省钱?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某地有两个村庄M,N,和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你确定该点.
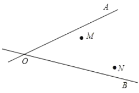
(2)如图,△ABC绕点C旋转后,顶点A旋转到了点D.

①指出这一旋转的旋转角;
②画出旋转后的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若![]() ,则
,则![]() ;②直角三角形的两个锐角互余:③如果
;②直角三角形的两个锐角互余:③如果![]() ,那么
,那么![]() ④
④![]() 个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() .
.
(1)求方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解满足![]() 为非正数,
为非正数,![]() 为负数,求
为负数,求![]() 的取值范围:
的取值范围:
(3)在(2)的条件下,当![]() 为何整数时,不等式
为何整数时,不等式![]() 的解集为
的解集为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
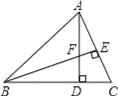
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com