
【题目】(1)某地有两个村庄M,N,和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你确定该点.
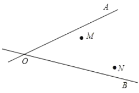
(2)如图,△ABC绕点C旋转后,顶点A旋转到了点D.

①指出这一旋转的旋转角;
②画出旋转后的三角形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,(一张铁皮只能生产一种产品)
(1)向用多少张铁皮做盒身,多少张铁皮做盒底,可以正好用完190张铁皮并制成一批完整的盒子?
(2)这批盒子一共有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
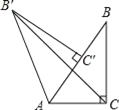
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB的度数.
小伟是这样思考的:如图2,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决.
请你回答:图1中∠APB的度数等于 .
参考小伟同学思考问题的方法,解决下列问题:
(1)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=1,PD=
,PB=1,PD=![]() ,则∠APB的度数等于 ,正方形的边长为 ;
,则∠APB的度数等于 ,正方形的边长为 ;
(2)如图4,在正六边形ABCDEF内有一点P,且PA=2,PB=1,PF=![]() ,则∠APB的度数等于 ,正六边形的边长为 .
,则∠APB的度数等于 ,正六边形的边长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com