
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB的度数.
小伟是这样思考的:如图2,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决.
请你回答:图1中∠APB的度数等于 .
参考小伟同学思考问题的方法,解决下列问题:
(1)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=1,PD=
,PB=1,PD=![]() ,则∠APB的度数等于 ,正方形的边长为 ;
,则∠APB的度数等于 ,正方形的边长为 ;
(2)如图4,在正六边形ABCDEF内有一点P,且PA=2,PB=1,PF=![]() ,则∠APB的度数等于 ,正六边形的边长为 .
,则∠APB的度数等于 ,正六边形的边长为 .

【答案】阅读材料:∠APB=∠AP′C=150°;(1)![]() (2)120°,
(2)120°,![]()
【解析】试题分析:根据旋转的性质结合勾股定理的逆定理,等边三角形的判定和性质即可得到结果;
(1)参照题目给出的解题思路,可将△ABP绕点A逆时针旋转90°,得到△A DP′,根据旋转的性质知:△ABP≌△A DP′,进而可判断出△APP′是等腰直角三角形,可得∠A P′P=45°;然后得到△DPP′是直角三角形,即可求得结果;
(2)方法同(2),再结合正六边形的性质即可求得结果.
由题意得△APP′是等边三角形,则∠A P′C=60°
∵![]()
∴△CPP′是直角三角形
∴∠CP′P=90°
∴∠AP′C=150°
∴∠APB=150°;
(1)将△ABP绕点A逆时针旋转90°,得到△A DP′,
由题得△ABP≌△A DP′,△APP′是等腰直角三角形,
∴∠AP′P=45°
∵![]()
∴△DPP′是直角三角形,![]()
∴∠DP′P=90°
∴∠DP′A=135°
∴∠APB=135°,正方形的边长为![]() ;
;
(2)方法同(2),∠APB的度数等于120°,正六边形的边长为![]()


科目:初中数学 来源: 题型:
【题目】甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:
s2甲、s 2乙、s 2丙分别表示三名运动员这次测试成绩的方差,下面各式中正确的是( )

A. s 2甲>s 2乙>s 2丙 B. s 2丙>s 2乙>s 2甲
C. s 2丙>s 2甲>s 2乙 D. s 2乙>s 2甲>s 2丙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() .
.
(1)在如图所示的平面直角坐标系中描出各点,画出![]() ;
;
(2)将![]() 先向左平移3个单位长度,再向下平移5个单位长度,得到
先向左平移3个单位长度,再向下平移5个单位长度,得到![]() , 请画出
, 请画出![]()
(3)求![]() 的面积;
的面积;
(4)设点![]() 在坐标轴上,且
在坐标轴上,且![]() 与
与![]() 的面积相等,请直接写出
的面积相等,请直接写出![]() 点的坐标
点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某地有两个村庄M,N,和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你确定该点.
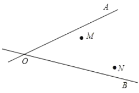
(2)如图,△ABC绕点C旋转后,顶点A旋转到了点D.

①指出这一旋转的旋转角;
②画出旋转后的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
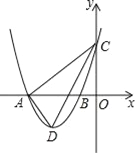
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(﹣4,0)、B(﹣l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ACD的面积为量求出S与m的函数关系式,并确定m为何值时S有最大值,最大值是多少?
(3)若点P是抛物线对称轴上一点,是否存在点P使得∠APC=90°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() .
.
(1)求方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解满足![]() 为非正数,
为非正数,![]() 为负数,求
为负数,求![]() 的取值范围:
的取值范围:
(3)在(2)的条件下,当![]() 为何整数时,不等式
为何整数时,不等式![]() 的解集为
的解集为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
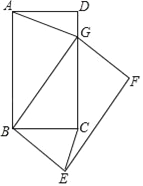
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com