
【题目】已知![]() .
.
(1)在如图所示的平面直角坐标系中描出各点,画出![]() ;
;
(2)将![]() 先向左平移3个单位长度,再向下平移5个单位长度,得到
先向左平移3个单位长度,再向下平移5个单位长度,得到![]() , 请画出
, 请画出![]()
(3)求![]() 的面积;
的面积;
(4)设点![]() 在坐标轴上,且
在坐标轴上,且![]() 与
与![]() 的面积相等,请直接写出
的面积相等,请直接写出![]() 点的坐标
点的坐标

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
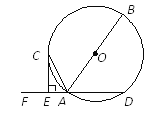
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导“低碳生活”,人们常选择以自行车作为代步工具,如图是一辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45 cm和60 cm,且它们互相垂直,座杆CE的长为20 cm,点A,C,E在同一条直线上,且∠CAB=75°.(参考数据:sin 75°≈0.966,cos 75°≈0.259,tan 75°≈3.732)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1 cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
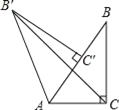
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
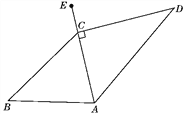
小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB的度数.
小伟是这样思考的:如图2,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决.
请你回答:图1中∠APB的度数等于 .
参考小伟同学思考问题的方法,解决下列问题:
(1)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=1,PD=
,PB=1,PD=![]() ,则∠APB的度数等于 ,正方形的边长为 ;
,则∠APB的度数等于 ,正方形的边长为 ;
(2)如图4,在正六边形ABCDEF内有一点P,且PA=2,PB=1,PF=![]() ,则∠APB的度数等于 ,正六边形的边长为 .
,则∠APB的度数等于 ,正六边形的边长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com