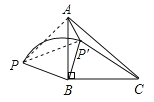
【题目】如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B＝135°，P′A∶P′C＝1∶3，则P′A∶PB＝( )
A. 1∶
B. 1∶2 C. 
∶2 D. 1∶
【答案】B
【解析】解：如图，连接AP，∵BP绕点B顺时针旋转90°到BP′，∴BP=BP′，∠ABP+∠ABP′=90°，又∵△ABC是等腰直角三角形，∴AB=BC，∠CBP′+∠ABP′=90°，∴∠ABP=∠CBP′，在△ABP和△CBP′中，∵BP=BP′，∠ABP=∠CBP′，AB=BC，∴△ABP≌△CBP′（SAS），∴AP=P′C，∵P′A：P′C=1：3，∴AP=3P′A，连接PP′，则△PBP′是等腰直角三角形，∴∠BP′P=45°，PP′=
PB，∵∠AP′B=135°，∴∠AP′P=135°﹣45°=90°，∴△APP′是直角三角形，设P′A=x，则AP=3x，根据勾股定理，PP′=
=
=
x，∴PP′=
PB=
x，解得PB=2x，∴P′A：PB=x：2x=1：2．故选B．
科目：初中数学 来源： 题型：
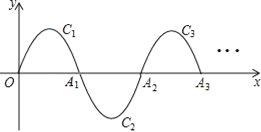
【题目】如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，得到Cn，若点P（2017，m）在抛物线Cn上，则m为（ ）
A. 1 B. ﹣1 C. 2 D. ﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，矩形ABCD中，AB＝
，AD＝4，在BC边上取点E，使BE＝AB，将△ABE向左平移到△DCF的位置，得到四边形AEFD．
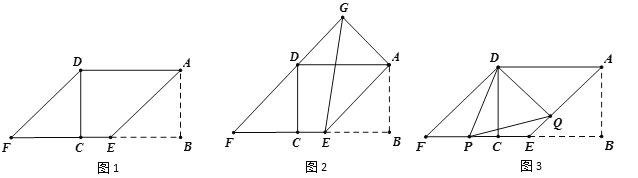
（1）求证：四边形AEFD是菱形；
（2）如图2，将△DCF绕点D旋转至△DGA，连接GE，求线段GE的长；
（3）如图3，设P、Q分别是EF、AE上的两点，且∠PDQ=67.5°，试探究线段PF、AQ、PQ之间的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在△ABC和△DCE中，∠ACB=∠DCE=90°，AC=DC，BC=EC，AB与DE相交于点F．
（1）如图1，求证AB=DE；
（2）如图2，连接CF，求证∠AFC=∠EFC；
（3）如图3，在（2）的条件下，当AF=EF时，连接BD，AE，延长CF交BD于点G，AE交CF于点H，若AE=8，BG=2，求线段GH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD为矩形，点E是边BC的中点，AF∥ED，AE∥DF
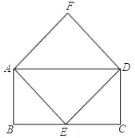
（1）求证：四边形AEDF为菱形；
（2）试探究：当AB：BC＝ ，菱形AEDF为正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
（1）若△ABC和△A1B1C1关于原点O成中心对称图形，画出△A1B1C1；
（2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2；
（3）在x轴上存在一点P，满足点P到点B1与点C1距离之和最小，请直接写出P B1+ P C1的最小值为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
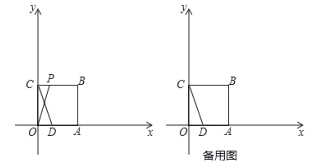
【题目】如图，在平面直角坐标系中，
是坐标原点，正方形
的顶点
、
分别在
轴与
轴上，已知正方形边长为3，点
为轴上一点，其坐标为
，连接
，点
从点出发以每秒1个单位的速度沿折线
的方向向终点运动，当点与点重合时停止运动，运动时间为
秒．
（1）连接
，当点在线段
上运动，且满足
时，求直线的表达式；
（2）连接
、
，求
的面积
关于的函数表达式；
（3）点在运动过程中，是否存在某个位置使得
为等腰三角形，若存在，直接写出点的坐标，若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE， 交 AC于点F.
(1)如图①，当
时，求
的值；
(2)如图②当DE平分∠CDB时，求证：AF=
OA；
(3)如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=
BG.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知菱形ABCD的对角线AC、BD相交于点O，延长AB至点E，使BE＝AB，连接CE．
（1）求证：四边形BECD是平行四边形；
（2）若∠E＝60°，AC＝
，求菱形ABCD的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com