
【题目】如图1,矩形ABCD中,AB=![]() ,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.
,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.
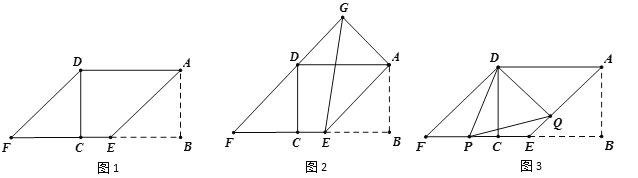
(1)求证:四边形AEFD是菱形;
(2)如图2,将△DCF绕点D旋转至△DGA,连接GE,求线段GE的长;
(3)如图3,设P、Q分别是EF、AE上的两点,且∠PDQ=67.5°,试探究线段PF、AQ、PQ之间的数量关系,并说明理由.
【答案】(1)见解析;(2)![]() ;(3)PQ2=PF2+AQ2,理由见解析
;(3)PQ2=PF2+AQ2,理由见解析
【解析】
(1)根据平移的性质得到AE∥DF,AE=DF,则由此判断四边形AEFD是平行四边形,然后由:邻边相等的平行四边形是菱形,证得结论;
(2)根据勾股定理,即可求解;(3)如下图,作辅助线,构建三角形全等,证明△PDQ≌△GDQ,得PQ=GQ,在Rt△AGQ中,根据勾股定理可得结论.
(1)由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵矩形ABCD,∴∠B=90°,∵BE=AE=![]() ,
,
∴AE=4,
又∵AE=AD=4,
∴四边形AEFD是菱形.
(2)由(1)得:△ABE是等腰直角三角形∴∠AEB=45°,
∵AE∥DF,
∴∠F=∠AEB=45°,
∵矩形ABCD,∴AD∥BC
∴∠DAE=∠AEB=45°,
∴∠GAE=90°,
∵△DCF绕点D旋转得到△DGA,
∴GA=CF=![]() ,
,
∴![]() .
.
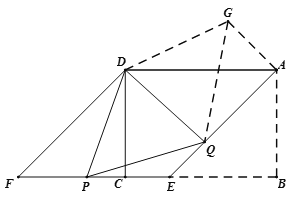
(3)PF、AQ、PQ之间的数量关系为:
PQ2=PF2+AQ2.
理由如下:
由(2)得:∠AEB=45°,∴∠ADF=∠AEF=135°,∵AD=DF,
∴将△DFP绕点D逆时针旋转135°得△DAG,
连GQ,如图,∴GA=PF,DG=DP,∠GDA=∠PDF,∠GAD=∠F=45°,
∴∠GAQ=∠GAD+∠DAE=90°,
∴GQ2=GA2+AQ2=PF2+AQ2;
又∵∠ADF=135°,而∠PDQ=67.5°,∴∠PDF+∠ADQ=135°﹣67.5°=67.5°,
∴∠GDA+∠ADQ=∠GDQ=67.5°,∴∠PDQ=∠GDQ
而DG=DP,DQ为公共边,∴△PDQ≌△GDQ,
∴PQ=GQ,
∴PQ2=PF2+AQ2.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=16cm,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动,当以B、P、D为顶点的三角形与以C、Q、P为顶点的三角形全等时,点Q的速度可能为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴有交点.
与x轴有交点.
(1)求m的取值范围;
(2)如果该二次函数的图像与x轴的交点分别为(x1,0),(x2,0),且2 x1 x2+ x1+ x2≥20,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.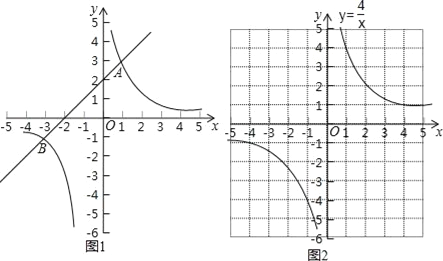
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量 | 1本 | 2本 | 3本 | 3本以上 |
人数(人) | 10 | 18 | 13 | 4 |
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<-1.5>=-1.解决下列问题:
(1)[-2.6]=______,<6.2>=______.
(2)已知x,y满足方程组 ,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的安全意识,某校组织了一次全校1500名学生都参加的“安全知识”考试,考题共10题.考试结束后,学校随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:

(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对10题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对超过7题的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com