
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.

【答案】(1)见解析;(2)14
【解析】
(1)根据题意可判断出四边形AODE是平行四边形,再由菱形的性质可得出AC⊥BD,即∠AOD=90°,继而可判断出四边形AODE是矩形;
(2)由菱形的性质和勾股定理求出OB,得出OA,由矩形的性质即可得出答案.
(1)证明:∵四边形ABCD是菱形,
∴∠AOD=90°.
又∵DE//AC,AE//BD,
∴四边形AODE是平行四边形.
∴四边形AODE是矩形.
(2)∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD=![]() BD=
BD=![]() ×8=4.
×8=4.
在Rt△AOB中,![]() .
.
在矩形AODE中,
DE=OA=3,AE=OD=4,
∴ OA+OD+DE+AE=14
即矩形AODE的周长为14.


科目:初中数学 来源: 题型:
【题目】已知![]() .
.
(1)在如图所示的平面直角坐标系中描出各点,画出![]() ;
;
(2)将![]() 先向左平移3个单位长度,再向下平移5个单位长度,得到
先向左平移3个单位长度,再向下平移5个单位长度,得到![]() , 请画出
, 请画出![]()
(3)求![]() 的面积;
的面积;
(4)设点![]() 在坐标轴上,且
在坐标轴上,且![]() 与
与![]() 的面积相等,请直接写出
的面积相等,请直接写出![]() 点的坐标
点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
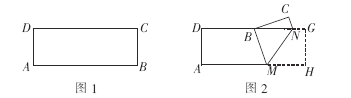
【题目】如图1,2在矩形纸片ABCD中,AD=6,AB=9.点M,N分别在AB,DC上(M不与A,B重合,N不与C,D重合),现以MN为折痕,将矩形纸片ABCD折叠.
(1)当B 点落在DC上时(如图2),求证:△MNB是等腰三角形;
(2)当B点与D点重合时,试求△MNB的面积;
(3)当B点与AD的中点重合时,试求折痕MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
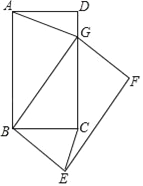
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
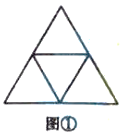
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com