
【题目】如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )

A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
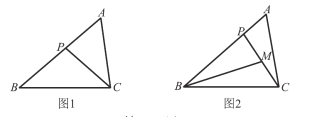
【题目】在△ABC中,P为边AB上一点.
(1)如图l,若∠ACP=∠B,求证:AC2 =AP·AB;
(2)若M为CP的中点,AC=2,如图2,若∠PBM=∠ACP,AB=3,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅要给-块长9米,宽7米的长方形地面铺瓷砖.如图,现有A和B两种款式的瓷砖,且A款正方形瓷砖的边长与B款长方形瓷砖的长相等, B款瓷砖的长大于宽.已知一块A款瓷砖和-块B款瓷砖的价格和为140元; 3块A款瓷砖价格和4块B款瓷砖价格相等.请回答以下问题:
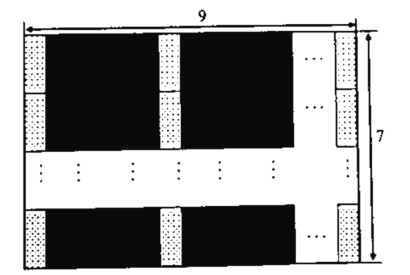

(1)分别求出每款瓷砖的单价.
(2)若李师傅买两种瓷砖共花了1000 元,且A款瓷砖的数量比B款多,则两种瓷砖各买了多少块?
(3)李师傅打算按如下设计图的规律进行铺瓷砖.若A款瓷砖的用量比B款瓷砖的2倍少14块,且恰好铺满地面,则B款瓷砖的长和宽分别为_ 米(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0;
(2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1;
(4)(x+3)2=(1﹣2x)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淮河汛期即将来临,防汛指挥部在一危险地带两岸各安置了-探照灯,便于夜间查看河面及两岸河堤的情况.如图,灯![]() 射线自
射线自![]() 顺时针旋转至
顺时针旋转至![]() 便立即回转,灯
便立即回转,灯![]() 射线自
射线自![]() 顺时针旋转至
顺时针旋转至![]() 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯![]() 转动的速度是
转动的速度是![]() /秒,灯
/秒,灯![]() 转动的速度是
转动的速度是![]() /秒,且
/秒,且![]() 满足:
满足:![]() 是
是![]() 的整数部分,
的整数部分,![]() 是不等式
是不等式![]() 的最小整数解.假定这- -带淮河两岸河堤是平行的,即
的最小整数解.假定这- -带淮河两岸河堤是平行的,即![]() ,且
,且![]() .
.

(1)如图1,![]() _____,
_____,![]() ;
;
(2)若灯![]() 射线先转动
射线先转动![]() 秒,灯
秒,灯![]() 射线才开始转动,在灯
射线才开始转动,在灯![]() 射线到达
射线到达![]() 之前,
之前,![]() 灯转动几秒,两灯的光東互相平行?
灯转动几秒,两灯的光東互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前。若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com