
【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0;
(2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1;
(4)(x+3)2=(1﹣2x)2.
【答案】(1)x1=![]() ,x2=
,x2=![]() (2)x1=2+
(2)x1=2+![]() ,x2=2﹣
,x2=2﹣![]() (3)x1=
(3)x1=![]() ,x2=
,x2=![]() (4)x1=﹣
(4)x1=﹣![]() ,x2=4
,x2=4
【解析】试题分析:(1)、利用公式法来进行求解,即![]() ,将a、b、c代入进行计算即可得出答案;(2)、利用配方法进行求解,得出方程的解;(3)、首先将方程整理成一般式,然后利用公式法求出方程的解;(4)、首先根据平方差公式将方程进行因式分解,然后求出方程的解.
,将a、b、c代入进行计算即可得出答案;(2)、利用配方法进行求解,得出方程的解;(3)、首先将方程整理成一般式,然后利用公式法求出方程的解;(4)、首先根据平方差公式将方程进行因式分解,然后求出方程的解.
试题解析:(1)x2﹣x﹣1=0; 这里a=1,b=﹣1,c=﹣1,
△=b2﹣4ac=(﹣1)2﹣4×1×(﹣1)=5. x=![]() =
=![]() ,
,
所以:x1=![]() ,x2=
,x2=![]() .
.
(2)移项,得x2﹣4x=1, 配方,得x2﹣4x+4=1+4, 即(x﹣2)2=5.
两边开平方,得x﹣2=±![]() , 即x=2±
, 即x=2±![]() , 所以x1=2+
, 所以x1=2+![]() ,x2=2﹣
,x2=2﹣![]() .
.
(3)x(x﹣2)﹣3x2=﹣1, 整理,得2x2+2x﹣1=0, 这里a=2,b=2,c=﹣1,
△=b2﹣4ac=22﹣4×2×(﹣1)=12.
x=![]() =
=![]() =
=![]() ,
,
即原方程的根为x1=![]() ,x2=
,x2=![]() .
.
(4)移项,得(x+3)2﹣(1﹣2x)
因式分解,得(x+3+1﹣2x)[x+3﹣(1﹣2x)]=0,
整理,得(3x+2)(﹣x+4)=0, 解得x1=﹣![]() ,x2=4.
,x2=4.


科目:初中数学 来源: 题型:
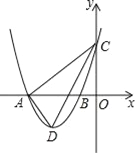
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(﹣4,0)、B(﹣l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ACD的面积为量求出S与m的函数关系式,并确定m为何值时S有最大值,最大值是多少?
(3)若点P是抛物线对称轴上一点,是否存在点P使得∠APC=90°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士的一位中学教师巴尔末从光谱数据![]() ,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
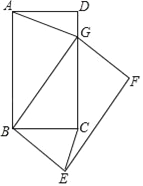
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点的坐标分别为A![]() ,B(2,0),直线AB与反比例函数
,B(2,0),直线AB与反比例函数![]() 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
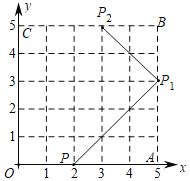
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com