练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】瑞士的一位中学教师巴尔末从光谱数据，…中，成功地发现了其规律，从而得到了巴尔末公式，继而打开了光谱奥妙的大门．请你根据这个规律写出第9个数_____．

    【答案】．

    【解析】

    分子的规律依次是：32，42，52，62，72，82，92…，分母的规律是：规律是：5+7=12 12+9=21 21+11=32 32+13=45…，即分子为（n+2）2，分母为n（n+4）．

    解：由题可知规律，第9个数的分子是（9+2）2=121；

    第五个的分母是：32+13=45；第六个的分母是：45+15=60；第七个的分母是：60+17=77；

    第八个的分母是：77+19=96；则第九个的分母是：96+21=117．

    因而第九个数是：．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．

    请结合以上信息解答下列问题：

    （1）m= ；

    （2）请补全上面的条形统计图；

    （3）在图2中，“乒乓球”所对应扇形的圆心角的度数为 ；

    （4）已知该校共有1200名学生，请你估计该校约有 名学生最喜爱足球活动．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李师傅要给-块长9米，宽7米的长方形地面铺瓷砖.如图，现有A和B两种款式的瓷砖，且A款正方形瓷砖的边长与B款长方形瓷砖的长相等, B款瓷砖的长大于宽.已知一块A款瓷砖和-块B款瓷砖的价格和为140元; 3块A款瓷砖价格和4块B款瓷砖价格相等.请回答以下问题:

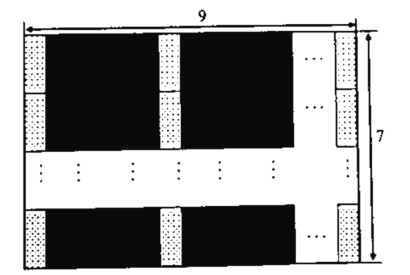
    (1)分别求出每款瓷砖的单价.

    (2)若李师傅买两种瓷砖共花了1000 元，且A款瓷砖的数量比B款多，则两种瓷砖各买了多少块?

    (3)李师傅打算按如下设计图的规律进行铺瓷砖.若A款瓷砖的用量比B款瓷砖的2倍少14块，且恰好铺满地面，则B款瓷砖的长和宽分别为_ 米(直接写出答案).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市自来水公司为限制单位用水，每月只给某单位计划内用水 3000 吨，计划内用水每吨收费 0.5元，超计划部分每吨按 0.8 元收费．

    （1）写出该单位水费 y（元）与每月用水量 x（吨）之间的函数关系式：（写出自变量取值范围）

    ①用水量小于等于 3000 吨 ；

    ②用水量大于 3000 吨 ．

    （2）某月该单位用水 3200 吨，水费是 元；若用水 2800 吨，水费 元．

    （3）若某月该单位缴纳水费 1580 元，则该单位用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：∠ACB＝90°，AC＝BC，AD⊥CM，BE⊥CM，垂足分别为D，E，

    （1）如图1，

    ①线段CD和BE的数量关系是　 ；

    ②请写出线段AD，BE，DE之间的数量关系并证明．

    （2）如图2，上述结论②还成立吗？如果不成立，请直接写出线段AD，BE，DE之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解下列方程．

    （1）x2﹣x﹣1=0；

    （2）x2﹣2x=2x+1；

    （3）x（x﹣2）﹣3x2=﹣1；

    （4）（x+3）2=（1﹣2x）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次自行车越野赛中，甲乙两名选手行驶的路程y（千米）随时间x（分）变化的图象（全程）如图，根据图象判定下列结论不正确的是（ ）

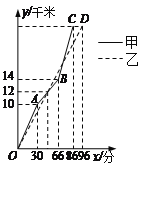
    A.甲先到达终点

    B.前30分钟，甲在乙的前面

    C.第48分钟时，两人第一次相遇

    D.这次比赛的全程是28千米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知 DE∥ BC， AE＝50cm， EC＝30cm， BC＝70cm，∠ BAC＝45°，∠ ACB＝40°.

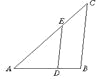
    求（1）∠ AED和∠ ADE的度数；（2） DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在平行四边形ABCD中,∠ABC=60°,AB=4,四条内角平分线围成四边形EFGH面积为，则平行四边形ABCD面积为________

    查看答案和解析>>

    同步练习册答案