
����Ŀ����ʦ��Ҫ��-�鳤9�ף���7�ij����ε����̴�ש.��ͼ������A��B���ֿ�ʽ�Ĵ�ש����A�������δ�ש�ı߳���B����δ�ש�ij����, B���ש�ij����ڿ�.��֪һ��A���ש��-��B���ש�ļ۸��Ϊ140Ԫ; 3��A���ש�۸��4��B���ש�۸����.��ش���������:
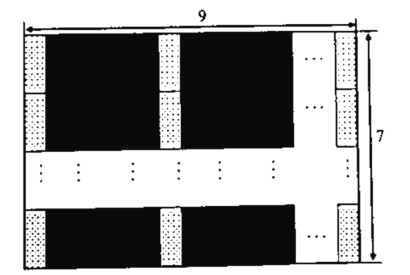

(1)�ֱ����ÿ���ש�ĵ���.
(2)����ʦ�������ִ�ש������1000 Ԫ����A���ש��������B��࣬�����ִ�ש�����˶��ٿ�?
(3)��ʦ�����㰴�������ͼ�Ĺ��ɽ����̴�ש.��A���ש��������B���ש��2����14�飬��ǡ���������棬��B���ש�ij��Ϳ��ֱ�Ϊ_ ��(ֱ��д����).
���𰸡���1��A���ש����Ϊ80Ԫ��B���Ϊ60Ԫ.��2������11��A���ש��2��B��;��8��A���ש��6��B��.��3��B���ש�ij��Ϳ��ֱ�Ϊ1��![]() ��1��
��1��![]() .
.
��������
��1����A���ש����xԪ��B���yԪ��������һ��A���ש��һ��B���ש�ļ۸��Ϊ140Ԫ��3��A���ש�۸��4��B���ש�۸�������г���Ԫһ�η����飬��⼴�ɣ�
��2����A������m�飬B������n�飬��m>n�����ݹ���1000 Ԫ�г���Ԫһ�η��̣������������������⼴�ɣ�
��3����A�������δ�ש�߳�Ϊa�ף�B�Ϊa�ף���b�ף�����ͼ���Լ���A���ש��������B���ש��2����14�������г��������a��ֵ��Ȼ����![]() �������̷�������b��ֵ.
�������̷�������b��ֵ.
��: (1)��A���ש����xԪ��B���yԪ��
����![]() ��
��
���![]() ��
��
��: A���ש����Ϊ80Ԫ��B���Ϊ60Ԫ��
(2)��A������m�飬B������n�飬��m>n��
��80m+60n=1000����4m+3n=50
��m��n����������m>n
��m=11ʱn=2��m=8ʱ��n=6��
������11��A���ש��2��B���ש��8��A���ש��6��B���ש��
(3)��A�������δ�ש�߳�Ϊa�ף�B�Ϊa�ף���b��.
������ã�![]() ��
��
���a=1.
�����֪��![]() ��������.
��������.
��![]() (k������)��
(k������)��
���εõ�![]() ��
��
��k=1ʱ��![]() ,�ʺ�ȥ)��
,�ʺ�ȥ)��
��k=2ʱ��![]() �� ����ȥ)��
�� ����ȥ)��
��k=3ʱ��![]() ��
��
��k=4ʱ��![]() ��
��
��: B���ש�ij��Ϳ��ֱ�Ϊ1��![]() ��1��
��1��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��ѧϰ����ʽ���̼���ⷨ�������У���ʦ���һ�����⣺������x�ķ�ʽ����![]() �Ľ�Ϊ��������a��ȡֵ��Χ��
�Ľ�Ϊ��������a��ȡֵ��Χ��
����С�齻�����ۺ�ͬѧ�����γ������������
С��˵�����������x�ķ�ʽ���̣��õ����̵Ľ�Ϊx=a��2��������ɵ�a��2��0������a��2����������
Сǿ˵���㿼�ǵIJ�ȫ�森�����뱣֤a��3���У�
��ʦ˵��Сǿ��˵��ȫ��ȷ��
��ش�С���������ⲻȫ�棬��Ҫ��������������Ҫ˵������ ����
����������⣺
��1����֪����x�ķ���![]() =1�Ľ�Ϊ��������m��ȡֵ��Χ��
=1�Ľ�Ϊ��������m��ȡֵ��Χ��
��2��������x�ķ�ʽ����![]() =��1�⣮ֱ��д��n��ȡֵ��Χ��
=��1�⣮ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AD�ǡ�BAC��ƽ���ߣ�DE��AB��E��F��AC�ϣ���BD=DF��
��1����֤��CF=EB��
��2�����ж�AB��AF��EB֮����ڵ�������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F������DF�����������ĸ����ۣ��١�AEF�ס�CAB����CF��2AF����DF��DC����tan��CAD��![]() ��������ȷ�Ľ�����( )
��������ȷ�Ľ�����( )

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��У�˻�֮ǰ���˽���꼶Ů��һ�������������÷����������Ϊ7�֣����ھ��꼶500��Ů����������60��Ů������һ�γ������ײ��������������±���
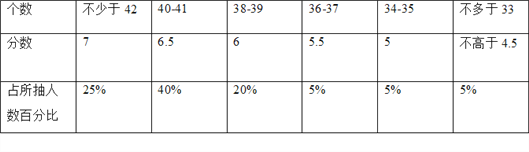
��1���ӱ��п��������ѧ�����õķ������ݵ�������______��
A.40% B.7 C.6.5 D.5%
��2���뽫����ͳ��ͼ����������
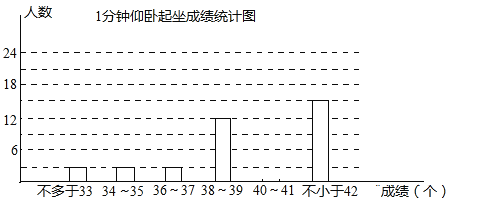
��3������������飬����Ƹ�У���Է���������6�ֵ��������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AC��BD�ཻ�ڵ�O���� AO=3����OBC=30�㣬����ε��ܳ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OP1A1B1��A1P2A2B2��A2P3A3B3��������An-1PnAnBn���������Σ��Խ���OA1��A1A2��A2A3��������An-1An����y���ϣ�n��1������������P1��x1��y1����P2��x2��y2����������Pn��xn��yn���ڷ���������y=![]() ��x��0����ͼ���ϣ�����֪B1��-1,1��.
��x��0����ͼ���ϣ�����֪B1��-1,1��.

��1����������y=![]() �Ľ���ʽ��
�Ľ���ʽ��
��2�����P2��P3�����ꣻ
��3���ɣ�1������2���Ľ��������Բ��벢ֱ��д������PnBnO�����Ϊ ����Pn������Ϊ______���ú�n��ʽ�ӱ�ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʿ��һλ��ѧ��ʦ�Ͷ�ĩ�ӹ�������![]() �����У��ɹ��ط���������ɣ��Ӷ��õ��˰Ͷ�ĩ��ʽ���̶����˹��װ���Ĵ��ţ���������������д����9����_____��
�����У��ɹ��ط���������ɣ��Ӷ��õ��˰Ͷ�ĩ��ʽ���̶����˹��װ���Ĵ��ţ���������������д����9����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����A��B�������ͽ���̨�ƣ���֪B�ͽ���̨��ÿյ���۱�A�͵Ķ�40Ԫ������3000Ԫ������A�ͽ���̨������5000Ԫ������B�ͽ���̨�Ƶ�������ͬ��
��1����ÿյA�ͽ���̨�ƵĽ����Ƕ���Ԫ��
��2���̳�������A��B���ͽ���̨��100յ�������ۣ�A�ͽ���̨��ÿյ���ۼ�Ϊ90Ԫ��B�ͽ���̨��ÿյ���ۼ�Ϊ140Ԫ����B�ͽ���̨�ƵĽ�������������A�ͽ���̨��������2����Ӧ������������ʹ�̳�������������̨��ʱ����ࣿ��ʱ�����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com