
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
【答案】(1):m<![]() 且m≠﹣
且m≠﹣![]() ;(2)n=1或n=
;(2)n=1或n=![]() .
.
【解析】
考虑分式的分母不为0,即分式必须有意义;
(1)表示出分式方程的解,由解为负数确定出m的范围即可;
(2)分式方程去分母转化为整式方程,根据分式方程无解,得到有增根或整式方程无解,确定出n的范围即可.
请回答:小明没有考虑分式的分母不为0(或分式必须有意义)这个条件;
(1)解关于x的分式方程得,x=![]() ,
,
∵方程有解,且解为负数,
∴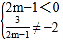 ,
,
解得:m<![]() 且m≠-
且m≠-![]() ;
;
(2)分式方程去分母得:3-2x+nx-2=-x+3,即(n-1)x=2,
由分式方程无解,得到x-3=0,即x=3,
代入整式方程得:n=![]() ;
;
当n-1=0时,整式方程无解,此时n=1,
综上,n=1或n=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务:
四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
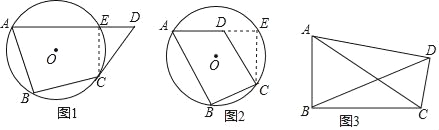
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是 .
(2)证明过程中主要体现了下列哪种数学思想: (填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.
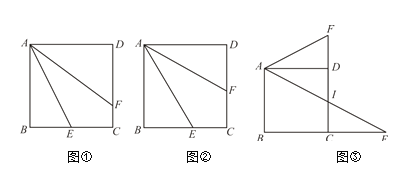
(1)如图①,当点E是线段BC的中点时,求证:AF=AB+CF;
(2)如图②,当∠BAE=30°时,求证:AF=2AB﹣2CF;
(3)如图③,当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(8)个图形有多少个正方体叠成( )

A.120个B.121个C.122个D.123个
查看答案和解析>>
科目:初中数学 来源: 题型:
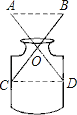
【题目】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅要给-块长9米,宽7米的长方形地面铺瓷砖.如图,现有A和B两种款式的瓷砖,且A款正方形瓷砖的边长与B款长方形瓷砖的长相等, B款瓷砖的长大于宽.已知一块A款瓷砖和-块B款瓷砖的价格和为140元; 3块A款瓷砖价格和4块B款瓷砖价格相等.请回答以下问题:
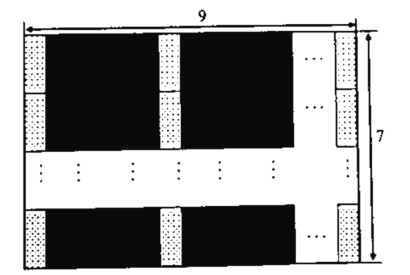

(1)分别求出每款瓷砖的单价.
(2)若李师傅买两种瓷砖共花了1000 元,且A款瓷砖的数量比B款多,则两种瓷砖各买了多少块?
(3)李师傅打算按如下设计图的规律进行铺瓷砖.若A款瓷砖的用量比B款瓷砖的2倍少14块,且恰好铺满地面,则B款瓷砖的长和宽分别为_ 米(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com