
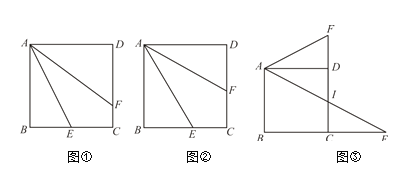
【题目】在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.
(1)如图①,当点E是线段BC的中点时,求证:AF=AB+CF;
(2)如图②,当∠BAE=30°时,求证:AF=2AB﹣2CF;
(3)如图③,当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析
【解析】
(1)由折叠的性质得出AG=AB,BE=GE,进而用HL判断出Rt△EGF≌Rt△ECF,代换即可得出结论;
(2)利用含30°的直角三角形的性质即可证明;
(3)先判断出△AIF为等边三角形,得出AI=FI=AF,再代换即可得出结论.
(1)如图,过点E作EG⊥AF于点G,连接EF.
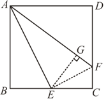
由折叠性质知,△ABE≌△AGE,
∴AG=AB,BE=GE,
∵BE=CE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
![]() ,
,
∴Rt△EGF≌Rt△ECF,(HL)
∴FG=FC,
∵AF=AG+FG,
∴AF=AB+FC ;
(2)如图,延长AF、BC交于点H.
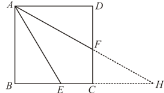
在正方形ABCD中,
∠B =90°,
由折叠性质知,∠BAE=∠HAE=30°,
∴∠H=90°-∠BAE-∠HAE =30°,
Rt△ABH中,∠B =90°,∠H =30°,
∴AH=2AB,
同理:FH=2FC,
∵AF=AH﹣FH,
∴AF=2AB﹣2FC;
(3)由折叠知,∠BAE=∠FAE=60°,
∴∠DAE=∠DAF=30°,
又∵AD⊥IF,
∴△AIF为等边三角形,
∴AF=AI=FI,
由(2)可得AE=2AB,
IE=2IC,
∵IC=FC-FI,
∴IC=FC-AF,
∴IE=2FC-2AF,
∵AI=AE-IE,
∴AF=2AB-(2FC-2AF)
=2FC-2AB.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负.![]() 年
年![]() 月
月![]() 日他办理了
日他办理了![]() 件业务:
件业务:![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元.
元.
![]() 若他早上领取备用金
若他早上领取备用金![]() 元,那么下班时应交回银行多少元?
元,那么下班时应交回银行多少元?
![]() 若每办一件业务,银行发给业务量的
若每办一件业务,银行发给业务量的![]() 作为奖励,那么这天小张应得奖金多少元?
作为奖励,那么这天小张应得奖金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,Rt△![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点.连结
上的一个动点.连结![]() ,过点
,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 交于点
交于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
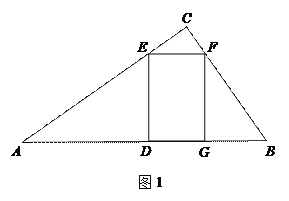
(1)如图1,当![]() ,点
,点![]() 在边
在边![]() 上时,求DE和EF的长;
上时,求DE和EF的长;
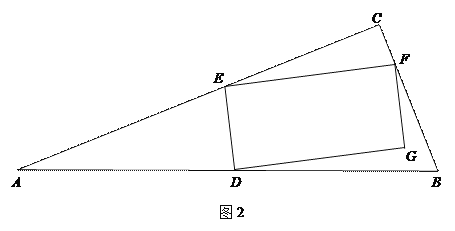
(2)如图2,若![]() ,设
,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求y关于
,求y关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,且点
,且点![]() 恰好落在Rt△
恰好落在Rt△![]() 的边上,求
的边上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)判断四边形![]() 是什么特殊四边形,并证明你的结论;
是什么特殊四边形,并证明你的结论;
(3)当![]() ________时,四边形
________时,四边形![]() 是正方形(只写结论,不需证明)
是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com