
【题目】(本题满分12分)如图,Rt△![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点.连结
上的一个动点.连结![]() ,过点
,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 交于点
交于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
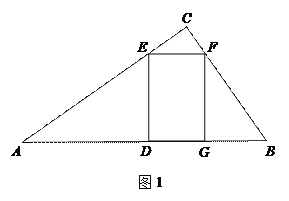
(1)如图1,当![]() ,点
,点![]() 在边
在边![]() 上时,求DE和EF的长;
上时,求DE和EF的长;
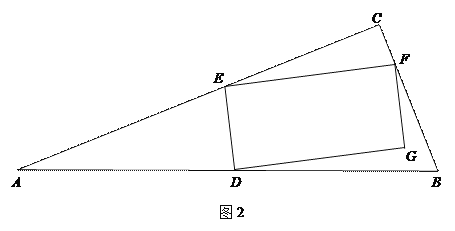
(2)如图2,若![]() ,设
,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求y关于
,求y关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,且点
,且点![]() 恰好落在Rt△
恰好落在Rt△![]() 的边上,求
的边上,求![]() 的长.
的长.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() ;(3)9或12.
;(3)9或12.
【解析】试题分析:(1)根据勾股定理求出AB,根据相似三角形的判定定理得到△ADE∽△ACB,根据相似三角形的性质求出DE和BG,求出EF;
(2)作DH⊥AC于H,根据相似三角形的性质得到y关于x的函数解析式;
(3)根据点G在边BC上和点G在边AB上两种情况,根据相似三角形的性质解答.
解:(1)∵∠ACB=90°,BC=6,AC=8,
∴AB= =10,
∵D为斜边AB的中点,
∴AD=BD=5,
∵DEFG为矩形,
∴∠ADE=90°,
∴∠ADE=∠C,又∠A=∠A,
∴△ADE∽△ACB,
∴AD:AC=DE:BC,即5:8=DE:6,
解得,DE=![]() ,
,
∵△ADE∽△FGB,
∴AD:GF=DE:BG,
则BG=![]() ,
,
∴EF=DG=AB-AD-BG=![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() , 从而
, 从而![]() .
.
易得△![]() ∽△
∽△![]() ,
,
由![]() , 可得
, 可得![]() ,
, ![]() .
.
所以![]() .
.
∴![]() .
.
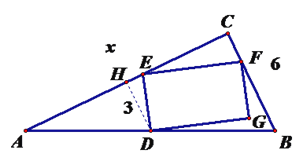
(3)由题意,点![]() 可以在边
可以在边![]() 或者
或者![]() 上.
上.
①若点![]() 在边
在边![]() 上,
上,
由![]() ,可知
,可知![]() ,于是
,于是![]() ;
;
②若点![]() 在边
在边![]() 上.
上.
记![]() ,矩形边长
,矩形边长![]() ,
,
由△![]() ∽△
∽△![]() , 可得
, 可得![]() , 即
, 即![]() ,
,
化简可得![]() , 因式分解后有:
, 因式分解后有: ![]() , 即
, 即![]() .
.
而由△![]() ∽△
∽△![]() , 所以
, 所以![]() , 从而
, 从而![]() .
.
综上知,AC的值为9或12.


科目:初中数学 来源: 题型:
【题目】二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5)
(1)求m的值,并写出二次函数的表达式;
(2)求出二次函数图象的顶点坐标、对称轴。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ,
, ![]() )
)
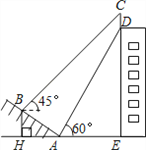
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
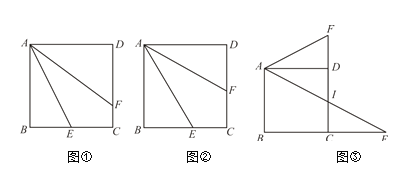
【题目】在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.
(1)如图①,当点E是线段BC的中点时,求证:AF=AB+CF;
(2)如图②,当∠BAE=30°时,求证:AF=2AB﹣2CF;
(3)如图③,当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
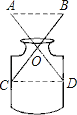
【题目】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能公交车
型两种环保节能公交车![]() 辆,若购买
辆,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元,若购买
万元,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)求购买购买![]() 型和
型和![]() 型公交车每辆多少钱?
型公交车每辆多少钱?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为![]() 万人次和
万人次和![]() 万人次,若该公司购买
万人次,若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过
型公交车的总费用不超过![]() 万元,且确保这
万元,且确保这![]() 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于![]() 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com