
【题目】如图,平行四边形ABCD的四个内角的平分线相交成四边形EFGH,求证:
(1)EG=HF.
(2)EG=BC-AB.
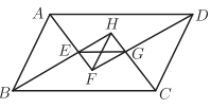
【答案】(1)见详解;(2)见详解.
【解析】
(1)利用三个内角等于90°的四边形是矩形,即可证明;
(2)延长AF交BC于M,通过全等得到AB=BM,然后证明四边形EMCG是平行四边形,得到EG=CM,即可得证.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,
∠BCD,
∴∠HBC+∠HCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形,
∴EG=HF;
(2)如图,延长AF交BC于M,
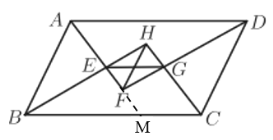
由(1)中可知AE⊥AF,即∠BEA=∠BEM=90°,
在Rt△ABE和Rt△MBE中,
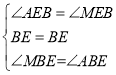 ,
,
∴△ABE≌△MBE,
∴AB=MB,AE=EM,
由于四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AB=CD
∵BH,DF分别平分∠ABC与∠ADC,
∴∠ABE=∠CDG,
在Rt△ABE和Rt△CDG中,
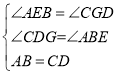 ,
,
∴△ABE≌△CDG,
∴CG=AE,
∴CG=EM,
由于四边形EFGH是矩形,
∴EM∥CG,
∴四边形EMCG是平行四边形,
∴EG=MC,
由于MC=BC-BM,
∴EG=BC-AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒![]() 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,∠l=∠2.

(1)求证:∠GFH与∠BHC互补;(2)若∠A=75°,FG⊥AC,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,Rt△![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点.连结
上的一个动点.连结![]() ,过点
,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 交于点
交于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
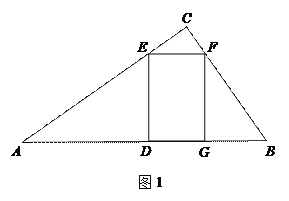
(1)如图1,当![]() ,点
,点![]() 在边
在边![]() 上时,求DE和EF的长;
上时,求DE和EF的长;
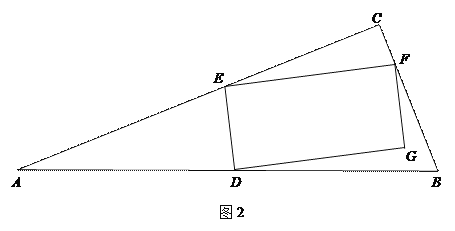
(2)如图2,若![]() ,设
,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求y关于
,求y关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,且点
,且点![]() 恰好落在Rt△
恰好落在Rt△![]() 的边上,求
的边上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com