
【题目】如图,小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m,台阶AC的坡度为1∶![]() ,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
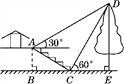
A. 6 m B. 7 m C. 8 m D. 9 m
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线![]() ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, ![]() (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
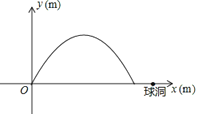
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:
s2甲、s 2乙、s 2丙分别表示三名运动员这次测试成绩的方差,下面各式中正确的是( )

A. s 2甲>s 2乙>s 2丙 B. s 2丙>s 2乙>s 2甲
C. s 2丙>s 2甲>s 2乙 D. s 2乙>s 2甲>s 2丙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:如图1,在![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() ;
;
发现:直角三角形中,如果有一个锐角等于![]() ,那么这个角所对的直角边等于斜边的_______.
,那么这个角所对的直角边等于斜边的_______.
应用:如图2,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1平行于直线l2,直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,DC∥AB交l4于点C.
(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的关系,并说明理由;

(2)当点D在l1、l2两线外侧运动时,试探究∠BAD、∠DEF、∠ADE之间的关系(点D和B、F不重合),画出图形,给出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边三角形ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.

(1)连接AQ、CP交于点M,则在P,Q运动的过程中,证明![]() ≌
≌![]() ;
;
(2)![]() 会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)P、Q运动几秒时,![]() 是直角三角形?
是直角三角形?
(4)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则![]() 变化吗?若变化说明理由,若不变,则求出它的度数。
变化吗?若变化说明理由,若不变,则求出它的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() .
.
(1)求方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解满足![]() 为非正数,
为非正数,![]() 为负数,求
为负数,求![]() 的取值范围:
的取值范围:
(3)在(2)的条件下,当![]() 为何整数时,不等式
为何整数时,不等式![]() 的解集为
的解集为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com