
【题目】请选择适当的方法解下列一元二次方程:
(1)![]()
(2)![]()
【答案】
(1)
x 2 4 = 0,
(x-2)(x+2)=0,
x1=2,x2=-2.
(2)
x ( x 6 ) = 5,
x2-6x-5=0,
x=![]()
x1=3![]() ,x2=
,x2=![]() .
.
【解析】(1)运用因式分解法或开方法都可以;
(2)采用公式法求解:![]() .
.
【考点精析】掌握直接开平方法和公式法是解答本题的根本,需要知道方程没有一次项,直接开方最理想.如果缺少常数项,因式分解没商量.b、c相等都为零,等根是零不要忘.b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方;要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之.


科目:初中数学 来源: 题型:
【题目】用公式法解﹣x2+3x=1时,先求出a、b、c的值,则a、b、c依次为( )
A.﹣1,3,1B.1,3,1C.﹣1,3,﹣1D.1,﹣3,﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
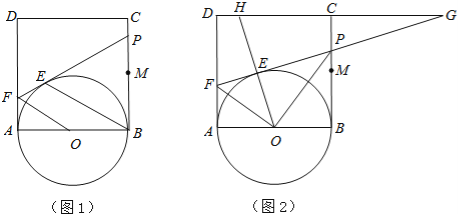
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程 ![]() 2-7
2-7 ![]() +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).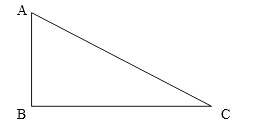
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为 ![]() 时运动时间t的值;
时运动时间t的值;
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com