
【题目】(本题满分6分)如图所示的方格地面上,标有编号1、2、3的3
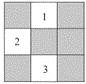
个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地
面完全相同.
(1)一只自由飞行的小鸟,将随意地落在图中所示的方格地面上,求
小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,
则编号为1、2的2个小方格空地种植草坪的概率是多少(用树状图或列表法求解)?
【答案】解: (1) 小鸟落在草坪上的概率为![]() 。
。
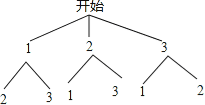
(2)用树状图列出所有可能的结果:
![]()
 开始
开始
![]()
![]()
![]()
![]()
![]()
![]() 1 2 3
1 2 3
2 3 1 3 1 2
所以编号为1、2的2个小方格空地种植草坪的概率是![]() 。
。
【解析】
试题根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用树状图分析时,一定要做到不重不漏.
试题解析:(1)P(小鸟落在草坪上)=![]()
(2)用树状图或列表格列出所有问题的可能的结果:
1 | 2 | 3 | |
1 | (1,2) | (1,3) | |
2 | (2,1) | (2,3) | |
3 | (3,1) | (3,2) |
由树状图(列表)可知,共有6种等可能结果,编号为1、2的2个小方格空地种植草坪有2种,
所以P(编号为1、2的2个小方格空地种植草坪)=![]()


科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)﹣a2b+(ab2﹣3a2b)﹣2(ab2﹣2a2b),其中a=2,b=1;
(2)2(a2﹣b)+3a2﹣2(a2+![]() b),其中(a2+m﹣1)2+|b+m+2|=0.
b),其中(a2+m﹣1)2+|b+m+2|=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
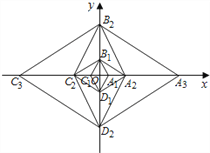
【题目】已知菱形A1B1C1D1的边长为2,且∠A1B1C1=60°,对角线A1C1,B1D1相较于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2 ,使得∠B1A2D1=60°;再以A2C2为对角线作菱形A2B2C2D2,使得∠A2B2C2=60°;再以B2D2为对角线作菱形B2C3D2A3,使得∠B2A3D2=60°…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点A2018的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
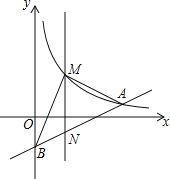
【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=![]() (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值;
(2)当t=4时,求△BMN面积;
(3)若MA⊥AB,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
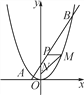
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 是边长为4的正方形点P为OA边上任意一点(与点
是边长为4的正方形点P为OA边上任意一点(与点![]() 不重合),连接CP,过点P作
不重合),连接CP,过点P作![]() ,且
,且![]() ,过点M作
,过点M作![]() ,交
,交![]() 于点
于点![]() 联结
联结![]() ,设
,设![]() .
.
(1)当![]() 时,点
时,点![]() 的坐标为( , )
的坐标为( , )
(2)设![]() ,求出
,求出![]() 与
与![]() 的函数关系式,写出函数的定义域。
的函数关系式,写出函数的定义域。
(3)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用
的坐标(用![]() 的式子表示)
的式子表示)
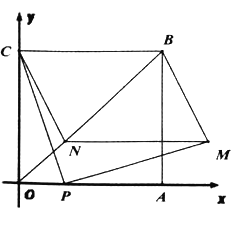
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm.现在将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,连接BB′,则BB′的长度为_____.
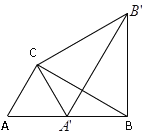
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究题
(1)观察下列有规律的数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …根据规律可知
…根据规律可知
①第10个数是________; ![]() 是第________个数.
是第________个数.
②计算![]() ________.(直接写出答案即可)
________.(直接写出答案即可)
(2)![]() 是不为1的有理数,我们把
是不为1的有理数,我们把![]() 称为
称为![]() 的差倒数.如:2的差倒数是
的差倒数.如:2的差倒数是![]() ,
,![]() 的差倒数是
的差倒数是![]() .已知
.已知![]() ,
,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,…,依此类推,
的差倒数,…,依此类推,![]() 是
是![]() 的差倒数,则
的差倒数,则![]() ________.
________.
(3)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如:[2.3]=2,[-1.5]=-2.则下列结论:①[-2.1]+[1]=-2; ②[x]+[-x]=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学拓展课上,老师让同学们探讨特殊四边形的做法:
如图,先作线段![]() ,作射线
,作射线![]() (
(![]() 为锐角),过
为锐角),过![]() 作射线
作射线![]() 平行于
平行于![]() ,再作
,再作![]() 和
和![]() 的平分线分别交
的平分线分别交![]() 和
和![]() 于点
于点![]() 和
和![]() ,连接
,连接![]() ,则四边形
,则四边形![]() 为菱形;
为菱形;
(1)你认为该作法正确吗?请说明理由.
(2)若![]() ,并且四边形
,并且四边形![]() 的面积为
的面积为![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() .请问图中存在这样的点
.请问图中存在这样的点![]() 吗?若存在,则求出
吗?若存在,则求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com