【题目】等腰三角形的周长为16，其一边长为6，则另两边为______．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
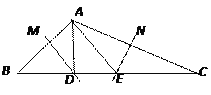
【题目】如图，△ABC中，边AB、AC的垂直平分线分别交BC于D、E．
（1）若BC＝10，则△ADE周长是多少？为什么？
（2）若∠BAC＝128°，则∠DAE的度数是多少？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，∠A=36°，DE是AB的垂直平分线，DE交AB于点D，交AC于点E，连接BE．下列结论①BE平分∠ABC；②AE=BE=BC；③△BEC周长等于AC+BC；④E点是AC的中点．其中正确的结论有 （填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【现场学习】
定义：我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”．
如：|x|=2，|2x﹣1|=3，|
|﹣x=1，…都是含有绝对值的方程．
怎样求含有绝对值的方程的解呢？基本思路是：含有绝对值的方程→不含有绝对值的方程．
我们知道，根据绝对值的意义，由|x|=2，可得x=2或x=﹣2．
[例]解方程：|2x﹣1|=3．
我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题．
解：根据绝对值的意义，得2x﹣1=3或2x﹣1= ．
解这两个一元一次方程，得x=2或x=﹣1．
检验：
（1）当x=2时，
原方程的左边=|2x﹣1|=|2×2﹣1|=3，
原方程的右边=3，
∵左边=右边
∴x=2是原方程的解．
（2）当x=﹣1时，
原方程的左边=|2x﹣1|=|2×（﹣1）﹣1|=3，
原方程的右边=3，
∵左边=右边
∴x=﹣1是原方程的解．
综合（1）（2）可知，原方程的解是：x=2，x=﹣1．
【解决问题】
解方程：||﹣x=1．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个月内，小丽的体重增长﹣1千克，意思就是这个月内（ ）
A． 小丽的体重减少﹣1千克
B． 小丽的体重增长1千克
C． 小丽的体重减少1千克
D．小丽的体重没变化
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的个数是( )
①一个有理数不是整数就是分数；②一个有理数不是正数就是负数；
③一个整数不是正的，就是负的；④一个分数不是正的，就是负的.
A. 1 B. 2 C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
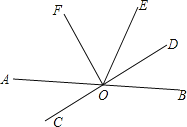
【题目】如图，直线AB与CD相交于点O，OD平分∠BOE，∠FOD=90°，问OF是∠AOE的平分线吗？请你补充完整小红的解答过程．
探究：
（1）当∠BOE=70°时，
∠BOD=∠DOE=
，
∠EOF=90°﹣∠DOE= °，
而∠AOF+∠FOD+∠BOD=180°，
所以∠AOF+∠BOD=180°﹣∠FOD=90°，
所以∠AOF=90°﹣∠BOD= °，
所以∠EOF=∠AOF，OF是∠AOE的平分线．
（2）参考上面（1）的解答过程，请你证明，当∠BOE为任意角度时，OF是∠AOE的平分线．
（3）直接写出与∠AOF互余的所有角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是∠AOB的边OB上的一点．
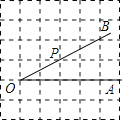
（1）过点P画OB的垂线，交OA于点C，
（2）过点P画OA的垂线，垂足为H，
（3）线段PH的长度是点P到 的距离，线段 是点C到直线OB的距离．
（4）因为直线外一点到直线上各点连接的所有线中，垂线段最短，所以线段PC、PH、OC这三条线段大小关系是 （用“＜”号连接）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
