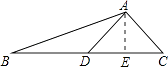
【题目】如图，AD是△ABC的中线，tanB= ，cosC= ，AC= ．求：
（1）BC的长；
（2）sin∠ADC的值．

参考答案：

【答案】
（1）解：过点A作AE⊥BC于点E，

∵cosC= ，

∴∠C=45°，

在Rt△ACE中，CE=ACcosC=1，

∴AE=CE=1，

在Rt△ABE中，tanB= ，即 = ，

∴BE=3AE=3，

∴BC=BE+CE=4


（2）解：∵AD是△ABC的中线，

∴CD= BC=2，

∴DE=CD﹣CE=1，

∵AE⊥BC，DE=AE，

∴∠ADC=45°，

∴sin∠ADC= ．


【解析】（1）过点A作AE⊥BC于点E，根据cosC= ，求出∠C=45°，求出AE=CE=1，根据tanB= ，求出BE的长即可；（2）根据AD是△ABC的中线，求出BD的长，得到DE的长，得到答案．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．

关闭