
【题目】已知关于x的方程x2 -(m+1)x+2(m-1)=0,
(1)求证:无论m取何值时,方程总有实数根;
(2)若等腰三角形腰长为4,另两边恰好是此方程的根,求此三角形的另外两条边长.
【答案】![]() 证明见解析
证明见解析![]() 4和2
4和2
【解析】
(1)根据方程的系数结合根的判别式即可得出△=(m-3)2≥0,由此即可证出结论;(2)由等腰三角形的性质可知b=c或b、c中有一个为4,①当b=c时,根据根的判别式△=(m-3)2=0,解之求出m值,将m的值代入原方程中解方程即可得出方程的解,再根据三角形的三边关系即可得出该种情况不合适;②当方程的一根为4时,将x=4代入原方程求出m值,将m的值代入原方程中解方程即可得出方程的解,再根据三角形的三边关系确定△ABC的三条边,结合三角形的周长即可得出结论.
(1)证明:∵△=[﹣(m+1)]2﹣4×2(m﹣1)=m2﹣6m+9=(m﹣3)2≥0,
∴无论m取何值,这个方程总有实数根;
(2)若腰长为4,将x=4代入原方程,得:16﹣4(m+1)+2(m﹣1)=0,
解得:m=5,
∴原方程为x2﹣6x+8=0,
解得:x1=2,x2=4.
组成三角形的三边长度为2、4、4;
若底边长为4,则此方程有两个相等实数根,
∴△=0,即m=3,
此时方程为x2﹣4x+4=0,
解得:x1=x2=2,
由于2+2=4,不能构成三角形,舍去;
所以三角形另外两边长度为4和2.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E. 
(1)求证:CD=BE;
(2)如果∠E=60°,CE=m,请写出求菱形ABCD面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一单杆高2.2m,两立柱之间的距离为1.6m,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状. 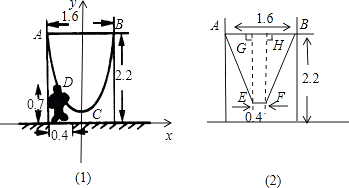
(1)一身高0.7m的小孩站在离立柱0.4m处,其头部刚好触上绳子,求绳子最低点到地面的距离;
(2)为供孩子们打秋千,把绳子剪断后,中间系上一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,求这时木板到地面的距离.(供选用数据: ![]() ≈1.8,
≈1.8, ![]() ≈1.9,
≈1.9, ![]() ≈2.1)
≈2.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为 ![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为 ![]() m,
m, ![]() m.
m. 
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)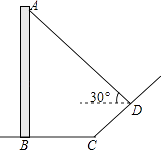
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果△ABC和△DEF这两个三角形全等,点C和点E,点B和点D分别是对应点,则另一组对应点是________,对应边是______________,对应角是_____________,表示这两个三角形全等的式子是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,∠A=36°,∠ABC=∠ACB,∠1=∠2,∠3=∠4,BD与CE交于点O,则图中等腰三角形有( )

A. 6个 B. 7个 C. 8个 D. 9个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com