
 如图,设P是等边△ABC内的一点,PA=3,PB=5,PC=4,则∠APC=150°°.
如图,设P是等边△ABC内的一点,PA=3,PB=5,PC=4,则∠APC=150°°. 分析 将△ABP绕点A逆时针旋转60°得△CEA,根据旋转的性质得EC=BP=5,AE=AP=4,∠PAE=60°,则△APE为等边三角形,得到PE=PA=3,∠APE=60°,在△EPC中,PE=3,PC=4,EC=5,根据勾股定理的逆定理可得到△EPC为直角三角形,且∠CPE=90°,即可得到∠APC的度数.
解答 解:∵△ABC为等边三角形,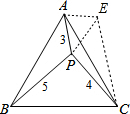
∴BA=BC,
可将△ABP绕点A逆时针旋转60°得△CEA,
连EP,如图,
∴EC=BP=5,AE=AP=4,∠PAE=60°,
∴△APE为等边三角形,
∴PE=PA=3,∠APE=60°,
在△EPC中,PE=3,PC=4,EC=5,
∴CE2=PE2+PC2,
∴△EPC为直角三角形,且∠CPE=90°,
∴∠APC=90°+60°=150°.
故答案为150°.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的判定与性质以及勾股定理的逆定理.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
 如图是函数y=$\frac{3}{x}$与函数y=$\frac{6}{x}$在第一象限内的图象,点P是y=$\frac{6}{x}$的图象上一动点,PA⊥x轴于点A,交y=$\frac{3}{x}$的图象于点C,PB⊥y轴于点B,交y=$\frac{3}{x}$的图象于点D.
如图是函数y=$\frac{3}{x}$与函数y=$\frac{6}{x}$在第一象限内的图象,点P是y=$\frac{6}{x}$的图象上一动点,PA⊥x轴于点A,交y=$\frac{3}{x}$的图象于点C,PB⊥y轴于点B,交y=$\frac{3}{x}$的图象于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
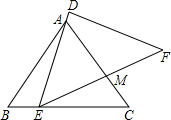 如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=1或$\frac{11}{6}$.
如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=1或$\frac{11}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班同学的身高情况 | B. | 了解全市每天丢弃的废旧电池数 | ||
| C. | 了解50发炮弹的杀伤半径 | D. | 了解我省农民的年人均收入情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com