
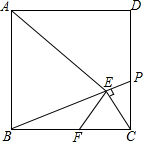
 正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F
正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F 分析 (1)根据余角的性质得到∠AEB=∠FEC,由正方形的性质得到∠ABC=∠BCD=90°,根据同角的余角相等得到∠ECF=∠BPC,由平行线的性质得到∠ABE=∠BPC,即可得到结论;
(2)根据相似三角形的性质得到$\frac{BE}{CE}=2$,通过△CPE∽△BCE,得到$\frac{CP}{BC}=\frac{CE}{BE}$=$\frac{1}{2}$,代入数据即可得到结论.
解答 (1)证明:∵CE⊥BP,EF⊥AE,
∴∠AEB+∠BEF=∠BEF+∠FEC,
∴∠AEB=∠FEC,
正方形ABCD中,
∵∠ABC=∠BCD=90°,
∴∠EPC+∠ECP=∠BCE+∠ECP=90°,
∴∠ECF=∠BPC,
∵AB∥CD,
∴∠ABE=∠BPC,
∴∠ABE=∠ECF,
∴△ABE∽△CEF;
(2)∵△ABE∽△CEF,△ABE的周长是△FCE周长2倍,
∴$\frac{BE}{CE}=2$,
∵∠CBE=∠ECP,∠BEC=∠CEP,
∴△CPE∽△BCE,
∴$\frac{CP}{BC}=\frac{CE}{BE}$=$\frac{1}{2}$,
∵BC=AB=8,
∴CP=4.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
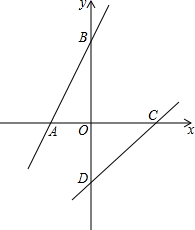 直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.
直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com