
【题目】在△ABC中,AB=AC,∠BAC=60°,点E为直线AC上一点,D为直线BC上的一点,且DA=DE. 当点D在线段BC上时,如图①,易证:BD+AB=AE;
当点D在线段CB的延长线上时,如图②、图③,猜想线段BD,AB和AE之间又有怎样的数量关系?写出你的猜想,并选择一种情况给予证明.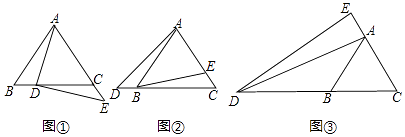
【答案】解;如图②中, 
结论:BD+AE=AB.
理由:作EM∥AB交BC于M,
∵△ABC是等边三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,
∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,
∴△CME是等边三角形,
∴CE=CM=EM,∠EMC=60°,
∴AE=BM,
∵DA=DE,
∴∠DAE=∠DEA,
∴∠BAC+∠DAB=∠C+∠EDM,
∴∠DAB=∠EDM,
∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,
∴∠ABD=∠DME,
在△ABD和△DEM中,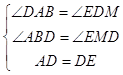 ,
,
∴△ABD≌△DEM,
∴DB=EM=CM,
∴DB+AE=CM+BM=BC=AB.
如图③中,
结论:BD﹣AE=AB.
理由:作EM∥AB交BC于M,
∵△ABC是等边三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,
∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,
∴△CME是等边三角形,
∴CE=CM=EM,∠EMC=∠MEC=60°,
∴AE=BM,
∵DA=DE,
∴∠DAE=∠DEA,
∴∠C+∠ADC=∠MEC+∠EDDEM,
∴∠ADB=∠DEM,
∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,
∴∠ABD=∠DME,
在△ABD和△DEM中,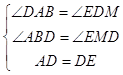 ,
,
∴△ABD≌△DME,
∴DB=EM=CM,
∴DB﹣AE=CM﹣BM=BC=AB.
【解析】图②中,论:BD+AE=AB,作EM∥AB交BC于M,先证明△EMC是等边三角形得CE=CM,AE=BM,再证明△ABD≌△DEM,得DB=EM=MC由此可以对称结论.图③中,结论:BD﹣AE=AB,证明方法类似.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O﹣A﹣B﹣C﹣D…,点P从点O出发沿着折线以每秒 ![]() 的速度向右运动,2016秒时,点P的坐标是 .
的速度向右运动,2016秒时,点P的坐标是 . 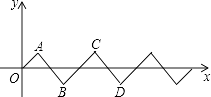
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题. 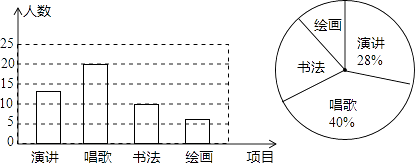
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) 
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 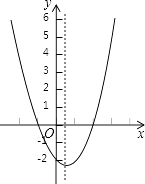
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com