
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)求证:该方程有两个实数根;
(2)如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;
(3)在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在﹣3≤x≤﹣ ![]() 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
【答案】
(1)证明:由根的判别式,可得:△=(3m+1)2﹣4×m×3=(3m﹣1)2,
∵(3m﹣1)2≥0,
∴△≥0,
∴原方程有两个实数根
(2)解:令y=0,那么mx2+(3m+1)x+3=0,
解得:x1=﹣3,x2=﹣ ![]() ,
,
∵抛物线与x轴两个交点的横坐标均为整数,且m为正整数,
∴m=1,
∴抛物线的解析式为:y=x2+4x+3;
(3)解:如图,

∵当x=0时,y=3,
∴C(0,3),
∵当y=0时,x1=﹣3,x2=﹣1,
又∵点A在点B的左侧,
∴A(﹣3,0),B(﹣1,0),
∵点D与点B关于y轴对称,
∴D(1,0),
设直线CD的解析式为:y=kx+b,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线CD的表达式为:y=﹣3x+3,
又∵当x=﹣ ![]() 时,y=
时,y= ![]() ,
,
∴点E(﹣ ![]() ,
, ![]() ),
),
∴平移后,点A,E的对应点分别为A′(﹣3+n,0),E′(﹣ ![]() +n,
+n, ![]() ),
),
当直线y=﹣3x+3经过点A′(﹣3+n,0)时,得:﹣3(﹣3+n)+3=0,解得:n=4,
当直线y=﹣3x+3经过点E′(﹣ ![]() +n,
+n, ![]() ),时,得:﹣3(﹣
),时,得:﹣3(﹣ ![]() +n)+3=
+n)+3= ![]() ,解得:n=
,解得:n= ![]() ,
,
∴n的取值范围是 ![]() ≤n≤4.
≤n≤4.
【解析】(1)要证一元二次方程有两个实数根,须证判别式△![]() 0;(2)先解方程,其中一根
0;(2)先解方程,其中一根![]() 为整数,m=1;(3)可用n的代数式表示出抛物线上两点平移后的坐标,代入直线解析式,可求出范围.
为整数,m=1;(3)可用n的代数式表示出抛物线上两点平移后的坐标,代入直线解析式,可求出范围.
【考点精析】认真审题,首先需要了解二次函数图象的平移(平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减),还要掌握抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图像交
的图像交 ![]() 轴于
轴于 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() ,连接直线
,连接直线 ![]() .
.
(1)求二次函数的解析式;
(2)点 ![]() 在二次函数的图像上,圆
在二次函数的图像上,圆 ![]() 与直线
与直线 ![]() 相切,切点为
相切,切点为 ![]() .
.
①若 ![]() 在
在 ![]() 轴的左侧,且△
轴的左侧,且△ ![]() ∽△
∽△ ![]() ,求点
,求点 ![]() 的坐标;
的坐标;
②若圆 ![]() 的半径为4,求点
的半径为4,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两个口袋中,都装有三个相同的小球,分别标有数字1,2,3,小刚、小丽两人进行摸球游戏.游戏规则是:小刚从A袋中随机摸一个球,同时小丽从B袋中随机摸一个球,当两个球上所标数字之和为奇数时小刚赢,否则小丽赢.
(1)这个游戏对双方公平吗?通过列表或画树状图加以说明.
(2)若公平,请你改变本题的游戏规则,使其对小丽有利;若不公平,也请你改变本的题的游戏规则,使游戏对双方公平.(无论怎么设计,都请说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
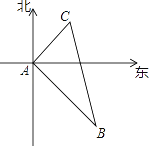
【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
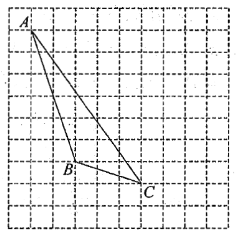
【题目】如图,在方格纸内将![]() 水平向右平移4个单位得到
水平向右平移4个单位得到![]() .
.
(1)补全![]() ,利用网格点和直尺画图;
,利用网格点和直尺画图;
(2)图中![]() 与
与![]() 的位置关系是: ;
的位置关系是: ;
(3)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(4)平移过程中,线段![]() 扫过的面积是: .
扫过的面积是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).

(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com