
| A. | -$\frac{7}{4}$ | B. | $\sqrt{3}$或-$\sqrt{3}$ | C. | 2或-$\sqrt{3}$ | D. | 2或-$\sqrt{3}$或-$\frac{7}{4}$ |
分析 求出二次函数对称轴为直线x=m,再分m<-2,-2≤m≤1,m>1三种情况,根据二次函数的增减性列方程求解即可.
解答 解:二次函数对称轴为直线x=m,
①m<-2时,x=-2取得最大值,-(-2-m)2+m2+1=4,
解得m=-$\frac{7}{4}$,不合题意,舍去;
②-2≤m≤1时,x=m取得最大值,m2+1=4,
解得m=±$\sqrt{3}$,
∵m=$\sqrt{3}$不满足-2≤m≤1的范围,
∴m=-$\sqrt{3}$;
③m>1时,x=1取得最大值,-(1-m)2+m2+1=4,
解得m=2.
综上所述,m=2或-$\sqrt{3}$时,二次函数有最大值4.
故选:C.
点评 本题考查了二次函数的最值,熟悉二次函数的性质及图象是解题的关键.


科目:初中数学 来源: 题型:解答题
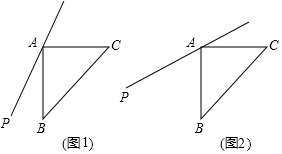
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
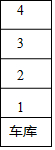 甲、乙两人同在如图所示的地下车库等电梯,两人到1至4层的任意一层出电梯,
甲、乙两人同在如图所示的地下车库等电梯,两人到1至4层的任意一层出电梯,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
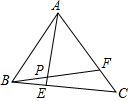 如图,△ABC中,E是BC上的一点,F是AC上一点,且3BE=BC,4CF=AF,AE、BF交于P点,如果△ABP的面积是30平方厘米,求△ABC的面积$\frac{120}{11}$.
如图,△ABC中,E是BC上的一点,F是AC上一点,且3BE=BC,4CF=AF,AE、BF交于P点,如果△ABP的面积是30平方厘米,求△ABC的面积$\frac{120}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com