

分析 (1)先求得∠AOE=100°,然后由角平分线的定义可知∠AOF=$\frac{1}{2}$∠AOE=50°,然后根据∠COF=∠AOF-∠AOC求解即可;
(2)当∠COF=35°时,如图①所示,由题意可知∠AOF=65°,由角平分线的定义可知∠AOE=130°,然后根据∠EOB=∠AOB-∠AOE=求解即可;当∠COF=10°时,应根据OF在∠AOC的内部和外部两种情况分类计算;
(3)与(2)的方法相同,依据OF在∠AOC的内部和外部两种情况分类计算即可.
解答 解:(1)∠AOE=∠AOB-∠EOB=140°-40°=100°.
∵OF平分∠AOE,
∴∠AOF=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×100°=50°.
∴∠COF=∠AOF-∠AOC=50°-30°=20°.
故答案为:50;20°.
(2)当∠COF=35°时,如图①所示: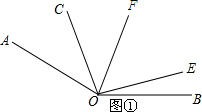
∵∠AOF=∠AOC+∠COF,
∴∠AOF=30°+35°=65°.
∵OF平分∠AOE,
∴∠AOE=2∠AOF=2×65°=130°.
∴∠EOB=∠AOB-∠AOE=140-130°=10°.
如图②所示:当∠COF=10°时.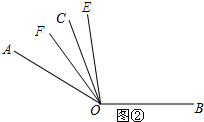
∵∠AOC=30°,∠COF=10°,
∴∠AOF=20°.
∵OF平分角∠AOE,
∴∠AOE=2∠AOF=40°.
∴∠BOE=∠AOB-∠AOE=140°-40°=100°.
如图③所示:当∠COF=10°时.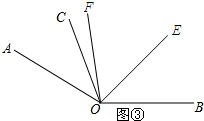
∵∠AOC=30°,∠COF=10°,
∴∠AOF=40°.
∵OF平分角∠AOE,
∴∠AOE=2∠AOF=80°.
∴∠BOE=∠AOB-∠AOE=140°-80°=60°.
∴∠BOE的度数为100°或60°.
(3)如图②所示:
∵∠AOC=30°,∠COF=n°,
∴∠AOF=(30-n)°.
∵OF平分角∠AOE,
∴∠AOE=2∠AOF=(60-2n)°.
∴∠BOE=∠AOB-∠AOE=140°-(60-2n)°=(80+2n)°.
如图③所示:
∵∠AOC=30°,∠COF=n°,
∴∠AOF=(30+n)°.
∵OF平分角∠AOE,
∴∠AOE=2∠AOF=(60+2n)°.
∴∠BOE=∠AOB-∠AOE=140°-(60+2n)°=(80-2n)°.
综上所述,∠EOB=(80-2n)°或(80+2n)°.
点评 本题主要考查的是角的计算,根据OF的位置进行分类讨论是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题

| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
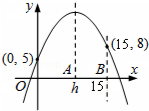 已知二次函数y=a(x-h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )
已知二次函数y=a(x-h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60元 | B. | 80元 | C. | 120元 | D. | 180元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在直角三角形中,30°角所对的直角边y与斜边x之间的关系 | |
| B. | 在等腰三角形中,顶角y与底角x之间的关系 | |
| C. | 圆的面积S与它的直径d之间的关系 | |
| D. | 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com