
 如图,AB是⊙O的直径,E为⊙O上一点,EF⊥AB于E,连接OE,AC∥OE,OD⊥AC于D,若BF=2,EF=4,求线段AC长.
如图,AB是⊙O的直径,E为⊙O上一点,EF⊥AB于E,连接OE,AC∥OE,OD⊥AC于D,若BF=2,EF=4,求线段AC长.  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
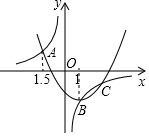 如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5.
如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点P是弦AC上一个动点(不与A、C重合),PE⊥AB,点E为垂足,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.
如图,AB是⊙O的直径,点P是弦AC上一个动点(不与A、C重合),PE⊥AB,点E为垂足,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
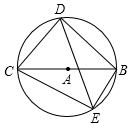 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
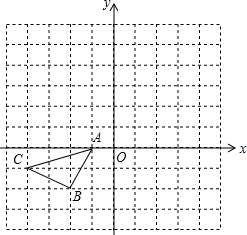 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com