
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了![]() 层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]()
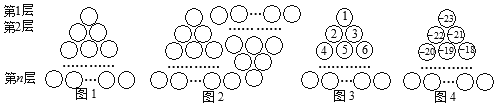
如果图中的圆圈共有13层,请解决下列问题:
(1)若自上往下,在图①每个圆圈中填上一串连续的正整数1,2,3,4,…,得到图3,写出第11层最左边这个圆圈中的数;
(2)若自上往下,在图①每个圆圈中填上一串连续的整数-23,-22,-21,20,…,得到图4,写出第10层最右边圆圈内的数;
(3)根据以上规律,求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).
【答案】(1)56;(2)31;(3)220.
【解析】
(1)由第11层最左边这个圆圈中的数是第10层的最后一个数加1,根据公式计算出10层的圆圈数即可得答案;(2)由(1)可知10层的圆圈数,根据第一层的数字即可求出第10层最右边圆圈内的数;(3)利用(2)把所有数相加即可.
(1)∵第11层最左边这个圆圈中的数是第10层的最后一个数加1,
∴第11层最左边这个圆圈中的数是![]() +1=56.
+1=56.
(2)由(1)得10层共有![]() =55个圆圈,
=55个圆圈,
∵第一个圆圈的数字是-23,
∴第10层最右边圆圈内的数是-23+55-1=31.
(3)图4中10层共有55个数,其中23个负数,1个0,31个正数,
所以图4中所有圆圈中各数的和为:-(1+2+3+4+…+23)+(1+2+3+4+…+31)=220.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
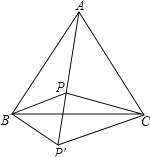
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
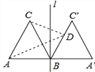
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)写出数轴上点A表示的数;
(2)将长方形OABC沿数轴向右水平移动,移动后的长方形记为![]() ,若移动后的长方形
,若移动后的长方形![]() 与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的
与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的![]() 时,写出数轴上点
时,写出数轴上点![]() 表示的数;
表示的数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形.
(2)若AC=8,EF=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.

(1,1),(3,1),(1,3),(1,1);
(-1,3),(-1,5),(-3,3),(-1,3);
(-5,1),(-3,-1),(-3,1),(-5,1);
(-1,-1),(1,-1),(-1,-3),(-1,-1).
(1)观察所得的图形,你觉得它像什么?
(2)求出这四个图形的面积和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com