
【题目】已知在![]() 中,
中,![]() ,过点
,过点![]() 引一条射线
引一条射线![]() ,
,![]() 是
是![]() 上一点.
上一点.
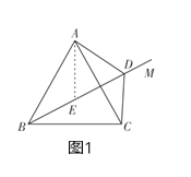
(1)如图1,![]() ,射线
,射线![]() 在
在![]() 内,
内,![]() ,求证:
,求证:![]() .
.
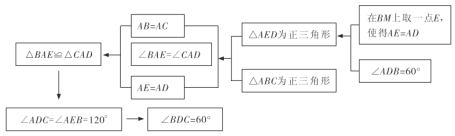
请根据以下思维框图,写出证明过程.
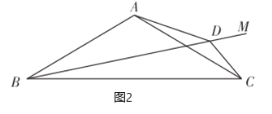
(2)如图2,已知![]() .
.
①当射线![]() 在
在![]() 内,求
内,求![]() 的度数.
的度数.
②当射线![]() 在
在![]() 下方,请问
下方,请问![]() 的度数会变吗?若不变,请说明理由;若改变,请直接写出
的度数会变吗?若不变,请说明理由;若改变,请直接写出![]() 的度数.
的度数.
(3)在第(2)题的条件下,作![]() 于点
于点![]() ,连结
,连结![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)①![]() ;②会变,
;②会变,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据SAS可证明 ![]() ,再利用三角形内角和即可得求证
,再利用三角形内角和即可得求证![]() 的度数为60°;
的度数为60°;
(2)①在![]() 上取一点
上取一点![]() ,
,![]() ,根据SAS可证明
,根据SAS可证明![]() ,再利用三角形内角和即可得求得
,再利用三角形内角和即可得求得![]() 的度数;
的度数;
②在![]() 延长线上取一点
延长线上取一点![]() ,使得
,使得![]() ,根据SAS可证明
,根据SAS可证明![]() ,再利用三角形内角和即可得求得
,再利用三角形内角和即可得求得![]() 的度数,与①进行比较即可得出答案;
的度数,与①进行比较即可得出答案;
(3)分当射线![]() 在
在![]() 内:作
内:作![]() ,可得△DCH是30°的直角三角形,可得CH的长度,即可得出△CDF的面积. 当射线
,可得△DCH是30°的直角三角形,可得CH的长度,即可得出△CDF的面积. 当射线![]() 在
在![]() 下方:由等腰三角形AED的性质可得
下方:由等腰三角形AED的性质可得![]() ,即可得出△CDF的面积.
,即可得出△CDF的面积.
解:(1)在![]() 上取一点
上取一点![]() ,使
,使![]() .
.
![]() ,
,![]() 是等边三角形.
是等边三角形.
![]() ,
,![]() ,
,
![]() 是正三角形,
是正三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
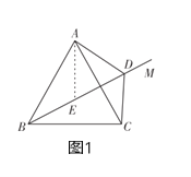
(2)①在![]() 上取一点
上取一点![]() ,
,![]() ,
,

![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
②会变.
在![]() 延长线上取一点
延长线上取一点![]() ,使得
,使得![]() ,
,
同理可得:![]() ,
,
![]() ,
,
![]() .
.
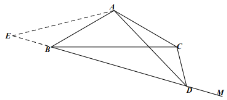
(3)当射线![]() 在
在![]() 内,如图,
内,如图,
![]()
![]() ,
,
且![]() ,
,![]() ,
,
![]() ,
,
作![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
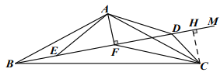
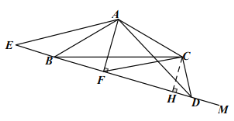
当射线![]() 在
在![]() 下方:如图,
下方:如图,
![]()
![]() ,
,
且![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读理解
材料一:已知在平面直角坐标系中有两点![]() ,
,![]() ,其两点间的距离公式为:
,其两点间的距离公式为:![]() ,当两点所在直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可化简为
,当两点所在直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可化简为![]() 或
或![]() ;
;
材料二:如图1,点![]() ,
,![]() 在直线
在直线![]() 的同侧,直线
的同侧,直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的值最小.解题思路:如图2,作点
的值最小.解题思路:如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交直线
交直线![]() 于
于![]() ,则点
,则点![]() ,
,![]() 之间的距离即为
之间的距离即为![]() 的最小值.
的最小值.

请根据以上材料解决下列问题:
(1)已知点![]() 在平行于
在平行于![]() 轴的直线上,点
轴的直线上,点![]() 在第二象限的角平分线上,
在第二象限的角平分线上,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图,在平面直角坐标系中,点![]() ,点
,点![]() ,请在直线
,请在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 最小,求出
最小,求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②当x>-1时y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c-m=0没有实数根,则m>2;⑤3a+c<0.其中,正确结论的序号是________________.
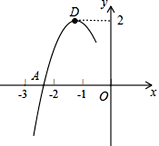
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
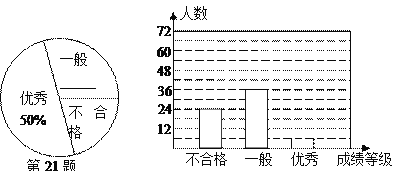
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com