
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不与点B重合),E在BO上,且∠BPE=![]() ,过点B作PE交PE的延长线于F,交AC于点G.
,过点B作PE交PE的延长线于F,交AC于点G.
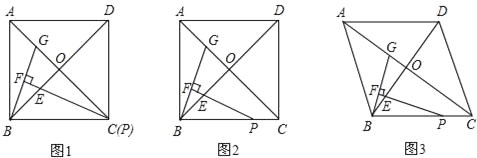
(1)当点P与点C重合时(如图1),填空△BOG≌_________,![]() =_________;
=_________;
(2)当点P不与点C重合时(图2),猜想:![]() 的值为_________.并证明你的结论;
的值为_________.并证明你的结论;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,则直接写出的值.
【答案】(1)△POE,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() tanα.
tanα.
【解析】
试题分析:(1)∵四边形ABCD是正方形,P与C重合,∴OB=OP,∠BOC=∠BOG=90°.∵PF⊥BG,∠PFB=90°,∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO.∴∠GBO=∠EPO.∴△BOG≌△POE(AAS).∴PE=BG,∵∠BPE=![]() ,∴∠BPE=∠GPF,∵PF⊥BG,∴BF=
,∴∠BPE=∠GPF,∵PF⊥BG,∴BF=![]() BG,∴
BG,∴![]() =
=![]() ,故答案为△POE,
,故答案为△POE,![]() ;
;
(2)证明如下:如图2,
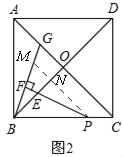
过P作PM∥AC交BG于M,交BO于N,∴∠PNE=∠BOC=90°,∠BPN=∠OCB.∵∠OBC=∠OCB=45°,∴∠NBP=∠NPB.∴NB=NP.∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,∴∠MBN=∠NPE.∴△BMN≌△PEN(ASA).∴BM=PE.∵∠BPE=![]() ∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.∵PF⊥BM,∴∠BFP=∠MFP=90°.∵PF=PF,∴△BPF≌△MPF(ASA).∴BF=MF,即BF=BM.∴BF=
∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.∵PF⊥BM,∴∠BFP=∠MFP=90°.∵PF=PF,∴△BPF≌△MPF(ASA).∴BF=MF,即BF=BM.∴BF=![]() PE,即:
PE,即:![]() =
=![]() .故答案为
.故答案为![]() ;
;
(3)如图2,过P作PM∥AC交BG于点M,交BO于点N,
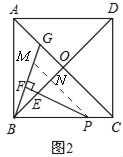
∴∠BPN=∠ACB=α,∠PNE=∠BOC=90°.由(2)同理可得,BF=BM,∠MBN=∠EPN. ∵∠BNM=∠PNE=90°,∴△BMN∽△PEN.∴![]() .在Rt△BNP中,tanα=
.在Rt△BNP中,tanα=![]() ,∴
,∴![]() =tanα,即:
=tanα,即:![]() =tanα.∴
=tanα.∴![]() =
=![]() tanα.
tanα.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】一元二次方程式x2﹣8x=48可表示成(x﹣a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )
A. 20 B. 12 C. ﹣12 D. ﹣20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,点A为![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
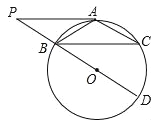
(1)求证:PA是⊙O的切线;
(2)若![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的![]() ,请完成下列问题:
,请完成下列问题:

(1)求本次抽取的学生人数;
(2)喜欢小说名著、喜欢童话故事的学生各有多少人?并补全条形统计图;
(3)全校共有2100名学生,请估计最喜欢“小说名著”的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合普查方法的是( )
A.了解一批灯泡的使用寿命
B.了解全国人民对湖南卫视“声人人心”栏目的收视率
C.了解全国中学生体重情况
D.了解某班学生对电影“我和我的祖国”的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若一图形各点的纵坐标不变,横坐标分别减5,则图形与原图形相比( )
A. 向右平移了5个单位长度 B. 向左平移了5个单位长度
C. 向上平移了5个单位长度 D. 向下平移了5个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com