
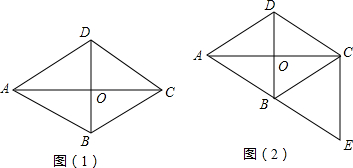
分析 (1)首先利用SSS定理证明△ABC≌△ADC可得∠BCA=∠DCA,再由等腰三角形的三线合一性质得出OB=OD,证出四边形ABCD是平行四边形,即可得出结论;
(2)由菱形的性质得出△ABC的面积=△ADC的面积=△ABD的面积=△BCD的面积,再由已知条件得出BE=AB,得出△ABC的面积=△ADC的面积=△ABD的面积=△BCD的面积=△BCE的面积,即可得出结果.
解答 (1)证明:在△ABC和△ADC中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{BC=DC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BCA=∠DCA,
∵BC=DC,
∴OB=OD,
又∵OC=OA,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形;
(2)解:图(2)中面积等于△BCE面积的三角形为△ABC、△ADC、△ABD、△BCD.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,
∴△ABC的面积=△ADC的面积=△ABD的面积=△BCD的面积,
∵BE=AD,AB=AD,
∴BE=AB,
∴△BCE的面积=△ABC的面积,
∴△ABC的面积=△ADC的面积=△ABD的面积=△BCD的面积=△BCE的面积,
∴图(2)中面积等于△BCE面积的三角形为△ABC、△ADC、△ABD、△BCD.
点评 此题主要考查了全等三角形的判定与性质,等腰三角形的性质,菱形的判定与性质;熟练掌握菱形的判定方法,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
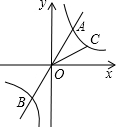 如图.过原点O的直线y=k1x和y=k2x与反比例$\frac{1}{x}$(x>0)的象分别交于点A、C.
如图.过原点O的直线y=k1x和y=k2x与反比例$\frac{1}{x}$(x>0)的象分别交于点A、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
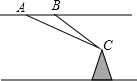 如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com