
分析 代入法的步骤:先选其中的一个方程用其中一个未知数表示另一个未知数,再代入另一个方程,从而达到消元的目的
解答 解:(1)解方程组$\left\{\begin{array}{l}{2x+y=3}&{①}\\{x+2y=-6}&{②}\end{array}\right.$,
由①得,y=3-2x ③,
将y=3-2x代入②,得:x+2(3-2x)=-6,解得:x=4,
将x=4代入③,得:y=3-2×4=-5,
故方程组的解为:$\left\{\begin{array}{l}{x=4}\\{y=-5}\end{array}\right.$;
(2)解方程组$\left\{\begin{array}{l}{x+5y=4}&{①}\\{3x-6y=5}&{②}\end{array}\right.$,
由①得:x=4-5y ③,
将③代入②得:3(4-5y)-6y=5,解得:y=$\frac{1}{3}$,
将y=$\frac{1}{3}$代入③,得:x=4-5×$\frac{1}{3}$=$\frac{7}{3}$,
故方程组的解为:$\left\{\begin{array}{l}{x=\frac{7}{3}}\\{y=\frac{1}{3}}\end{array}\right.$;
(3)解方程组$\left\{\begin{array}{l}{3x+y=8}&{①}\\{3x-y=4}&{②}\end{array}\right.$,
由①得:y=8-3x ③,
将③代入②得:3x-(8-3x)=4,解得:x=2,
将x=2代入③,得:y=8-3×2=2,
故方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$;
(4)解方程组$\left\{\begin{array}{l}{2x+5y=8}&{①}\\{x-3y=-2}&{②}\end{array}\right.$,
由②得,x=3y-2 ③,
将③代入①,得:2(3y-2)+5y=8,解得:y=$\frac{12}{11}$,
将y=$\frac{12}{11}$代入②得:x-$\frac{36}{11}$=-2,解得:x=$\frac{14}{11}$,
故方程组的解为:$\left\{\begin{array}{l}{x=\frac{14}{11}}\\{y=\frac{12}{11}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 360° | B. | 540° | C. | 630° | D. | 720° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.
如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
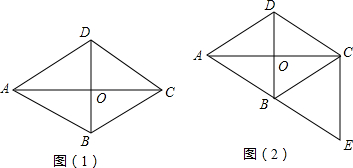
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
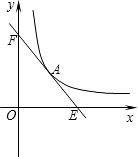 如图,已知:A(m,4)是一次函数y=kx+b与反比例函数y=$\frac{12}{x}$的公共点
如图,已知:A(m,4)是一次函数y=kx+b与反比例函数y=$\frac{12}{x}$的公共点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com