
【题目】(1)如图①,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是____;
(2)如图②,点A在B处北偏东40°方向,在C处北偏西45°方向,则∠BAC=____°.
(3)如图③,∠ABD和∠BDC的平分线交于点E,BE交AB于点F,∠1+∠2=90°,试说明:AB∥AB,并探究∠2与∠3的数量关系.
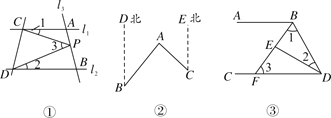
【答案】(1)∠1+∠2=∠3(2)85(3)见解析,∠2+∠3=90°
【解析】
(1)作PM∥AC.根据平行线间的传递性,得PM∥BD.再由平行线的性质,得∠1=∠CPM,∠2=∠MPD.所以,∠1+∠2=∠3.(2)由题可知∠BAC=∠B+∠C,所以,∠BAC=85°.(3)由题意,先证明AB∥AB.再通过角的变换,得到∠BED=∠DAB=90°,所以∠3+∠FDE=90![]() ,最后得到∠2+∠3=90.
,最后得到∠2+∠3=90.
(1)如答图,作PM∥AC,
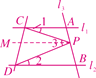
∵AC∥BD,∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
(2)由题可知∠BAC=∠B+∠C.
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
(3)证明:∵BE,DE分别平分∠ABD,∠BDC,
∴∠1=![]() ∠ABD,∠2=
∠ABD,∠2=![]() ∠BDC.
∠BDC.
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥AB.
∵DE平分∠BDC,
∴∠2=∠FDE.
∵∠1+∠2=90°,
∴∠BED=∠DAB=90°,
∴∠3+∠FDE=90°,
∴∠2+∠3=90°.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )

A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式_____;
(2)证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0)
=logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算log32+log36﹣log34=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 个单位长度的小正方形组成的网格中,
个单位长度的小正方形组成的网格中,![]() 、正方形
、正方形![]() 、正方形
、正方形![]() 的顶点均在格点上.
的顶点均在格点上.
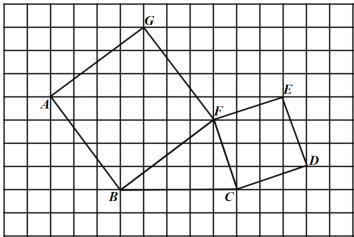
(1)以格点为原点,建立合适的平面直角坐标系,使得![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,则点
,则点![]() 的坐标为______,点
的坐标为______,点![]() 的坐标为_______;
的坐标为_______;
(2)利用面积计算线段![]() ________;
________;
(3)点![]() 为直线
为直线![]() 上一动点,求
上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为2,a2+1,则点P所在的象限是____;以方程组![]() 的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com